Vektorit ja matriisit
Voit ladata materiaalin tästä Jupyter Notebookina.
import math as mth
import numpy as np
Matriisit ja vektorit ovat keskeinen osa lineaarialgebraa. Lineaarialgebra puolestaan liittyy moderniin data scienceen ja koneoppimiseen keskeisesti nopeuttamalla/tehostamalla laskentaa vrt. perinteisiin menetelmiin, kuten for loopin käyttämiseen.
import random
l1 = random.sample(range(1, 100000000), 10000000) #Luodaan lista jossa on miljoona lukua
import time
t1=time.time()
l2= []
for item in l1:
l2.append((item)^2)
t2 = time.time()
print("With for loop and appending it took {} seconds".format(t2-t1))
With for loop and appending it took 1.8989009857177734 seconds
a1= np.array(l1)
t3=time.time()
a2=np.power(a1,2)
t4 = time.time()
print("With direct Numpy Power method it took {} seconds".format(t4-t3))
With direct Numpy Power method it took 0.04146313667297363 seconds
looptime = t2-t1
vectortime = t4-t3
print("Vektoritoteutus oli {} kertaa for loop toteusta nopeampi ".format(looptime/vectortime))
Vektoritoteutus oli 45.79733078794082 kertaa for loop toteusta nopeampi
Vektorit
Lukiomatematiikassa vektorit esitetään olioina, joilla on suunta ja pituus. Tason ja kolmiulotteisen avaruuden vektorit kirjoitetaan yleensä yksikkövektorien i,j ja k avulla. Eräs tason vektori voisi olla vaikkapa v = 3i -2j. Jokaisella koordinaatiston pisteellä on paikkavektori, jonka komponentit ovat pisteen koordinaatit. Esimerkiksi pisteen (3, −2) paikkavektori on edellä mainittu vektori v.
Data sciencessa vektorit voivat kuitenkin olla mitä tahansa “järjestettyjä” listoja. Vektori voi olla vaikkapa 1000 elementtiä sisältävä “lista”, mutta yleisimmin vektoria voisi kuvailla lukujonona.
Vektoreille voidaan suorittaa monia laskutoimituksia, kuten yhteen- ja vähennyslasku, kerto- ja jakolasku, ym. Jotta edellä mainitut laskutoimitukset onnistuvat, pitää vektorien olla elementeiltään saman mittaisia.
#Muodostetaan vektorit x ja y
x = np.array([2,2])
y = np.array([4,1])
#Vektorien ja matriisien muodostamisessa käytetään yleisesti numpy-kirjaston array() metodia.
print(x)
[2 2]
print(y)
[4 1]
type(x)
#Tarkastettaessa type() funktiolla x:n tyyppi, saadaan vastaukseksi array.
numpy.ndarray
Vektorien yhteenlasku
x+y
array([6, 3])
Geometrisesti tarkasteltuna vektorien yhteenlasku (2-ulotteisesti) tarkoittaa 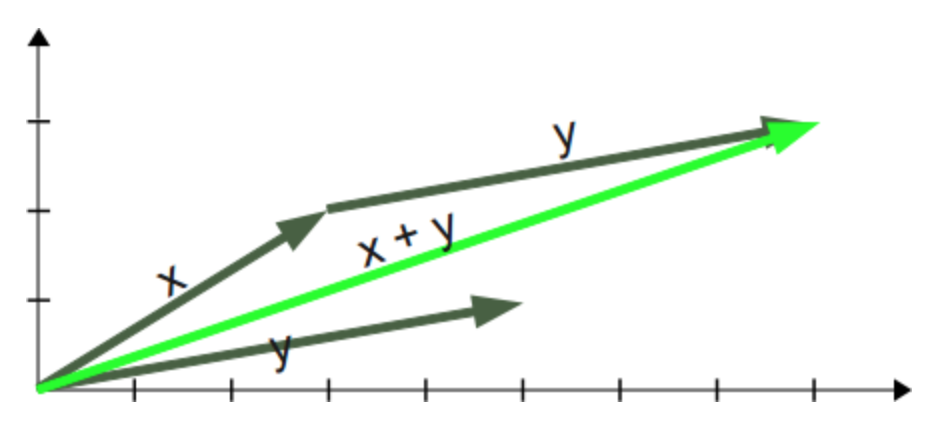
Vektorien vähennyslasku
Vektorien vähennyslasku x-y tarkoittaa samaa kuin x+(-y)
x-y
array([-2, 1])
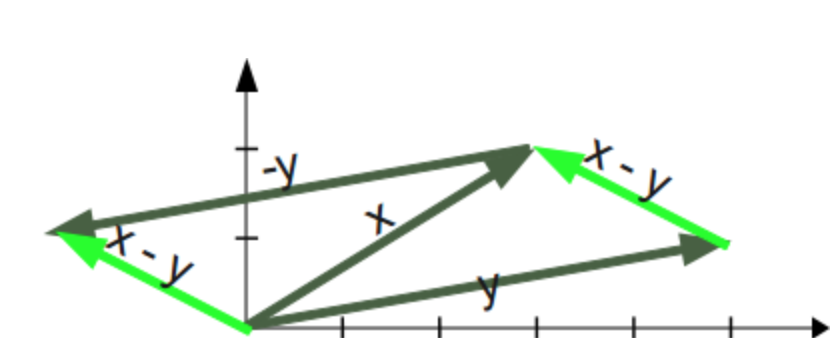
Vektorien kertolasku
Jos halutaan kertoa vektorit yhteen, niin se onnistuu tavallisella * -merkillä. Vektorien tulee jälleen olla elementeiltään saman mittaisia, ja jokainen vektorien elementti kerrotaan vastaavalla toisen vektorin elementillä (ie. element-wise multiplication)
x*y
array([8, 2])
Vektorien kertominen reaaliluvulla
Vektorin voi kertoa reaaliluvulla, ja lopputuloksena on vektori, jonka jokainen elementti on erikseen kerrottu e.m. reaaliluvulla.
print('vektori x')
print(x)
print('10 * x')
10*x
vektori x
[2 2]
10 * x
array([20, 20])
Pistetulo / Skalaaritulo
Vektorien pistetuloa käytetään koneoppimisessa laajasti. Pistetulo tarkoittaa, että vektorin a jokainen elementti kerrotaan vektorin b vastaavan elementin kanssa, ja kaikkien elementtien tulot lasketaan yhteen, jolloin lopputulokseksi tulee YKSI LUKU.

Pistetulon ominaisuuksia

Vektorin pituuden tarkistaminen
a = np.array([1,5,8,0,12,14,11,2,3,6,8,24,55,689,111,23,76,89,2,0,1,55,43,56,78,11])
#Kuinka monta elementtiä vektorissa a on?
len(a)
26
Matriisit
Matriiseja merkitään usein isolla kirjaimella, erotukseksi vektorista. Muuttujan nimellä ei sinänsä ole väliä. Matriiseja voi muodostaa Pythonilla usealla eri tavalla.
#Yksi tapa muodostaa matriisi
X = range(16)
X = np.reshape(X,(4,4))
print(X)
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
Matriisin voi luoda myös ns. nested list rakenteella
A = [[80,75,85,90,95],
[75,80,75,85,100],
[80,80,80,90,95]]
print(A)
[[80, 75, 85, 90, 95], [75, 80, 75, 85, 100], [80, 80, 80, 90, 95]]
Huom! Nyt matriisi A ei näytä matriisilta printattuna, mutta se on rakenteeltaan matriisi.
Y= [1,2,3,4,5,6,7,8,9]
Y = np.reshape(Y,(3,3))
print(Y)
[[1 2 3]
[4 5 6]
[7 8 9]]
Kaksi yleisintä tapaa muodostaa matriisi Pythonissa on käyttää joko numpy-kirjaston array()- tai matrix()-metodeja.
#Numpyn array() metodi, vektorien tapaan.
T = array([[10,11,12,13],
[5,6,7,8],
[1,2,3,3]])
print('T')
print(T)
U = array([[2,4],
[1,3],
[1,2],
[6,7]])
print('U')
print(U)
T
[[10 11 12 13]
[ 5 6 7 8]
[ 1 2 3 3]]
U
[[2 4]
[1 3]
[1 2]
[6 7]]
Matriisin muodostamiseen voi käyttää myös numpyn matrix() metodia. Riippuen siitä, kumpaa metodia (array- vai matrix) on käytetty, on vaikutusta sille, millä tavalla matriiseja voi myöhemmin kertoa.
Matrix-objekti on Numpyn array-objektin ns. aliluokka.
M = np.matrix( [[2,3], [3, 5]] )
N = np.matrix( [[1,2], [5,-1]] )
#Muodostuksessa ei sinänsä ole mitään eroa array() metodiin verrattuna.
#Lukuparien muodostuksessa käytettävien hakasulkeiden sijaan voi käyttää myös normaalia sulkeita,
# ts. [[1,2], [5,-1]] voi kirjoittaa myös ((1,2),(5,-1))
print('M')
print(M)
print('N')
print(N)
M
[[2 3]
[3 5]]
N
[[ 1 2]
[ 5 -1]]
type(N)
numpy.matrixlib.defmatrix.matrix
Matriisit ovat aina m x n -muotoisia, jossa m= rivien määrä ja n=sarakkaiden määrä.
Matriisien laskutoimituksia
Yhteen- ja vähennyslasku
Vain samanmuotoisia matriiseja voi laskea yhteen (tai vähentää toisistaan)

A = [80,75,85,90,95,100,200,101,95]
A = np.reshape(A,(3,3))
print('A')
print(A)
B = [10,69,77,90,95,100,34,100,11]
B = np.reshape(B,(3,3))
print('B')
print(B)
#A ja B ovat nyt 3 x 3 matriiseja.
A
[[ 80 75 85]
[ 90 95 100]
[200 101 95]]
B
[[ 10 69 77]
[ 90 95 100]
[ 34 100 11]]
#Elementit matriiseissa A ja B täsmäävät, joten matriisit voi laskea yhteen.
C =A+B
print('C')
print(C)
C
[[ 90 144 162]
[180 190 200]
[234 201 106]]
D= C-B
D==A
array([[ True, True, True],
[ True, True, True],
[ True, True, True]], dtype=bool)
E= B+A
Onko E(=B+A) sama matriisi kuin A+B?
Matriiseja voi myös kertoa. Matriisien kertolaskua (vakiolla) kutsutaan skalaarikertolaskuksi.

#Käytetään edellä muodostettua matriisia A, ja kerrotaan se reaaliluvulla, tässä tapauksessa kokonaisluvulla
10*A
array([[ 800, 750, 850],
[ 900, 950, 1000],
[2000, 1010, 950]])
#Reaaliluku voi olla myös rationaaliluku (murtoluku). Skalaarilla kerrottaessa ei ole väliä, onko se matriisin edessä
#vai takana.
A* 1/2
array([[ 40. , 37.5, 42.5],
[ 45. , 47.5, 50. ],
[ 100. , 50.5, 47.5]])
Matriisien kertolasku
Matriisin voi myös kertoa matriisilla. Tälle on kuitenkin erityisiä ehtoja, jotka poikkeavat normaalista kertolaskusta.
1) Kaksi matriisia voidaan kertoa keskenään vain, jos ensimmäisessä on yhtä paljon sarakkeita kuin toisessa on rivejä
2) Matriisien kertolaskussa kertomisjärjestyksellä ON väliä. AB ei ole sama kuin BA

A1 = array([[10,11,12,13],
[5,6,7,8],
[1,2,3,3]])
#Matriisissa A1 on 4 saraketta
B1 = array([[2,4],
[1,3],
[1,2],
[6,7]])
#Matriisissa B1 on 4 riviä
C1 = A1.dot(B1)
print(C1)
#Kun array-muotoisia matriiseja kerrotaan Pythonissa keskenään, käytetään joko dot metodia
#(tai numpyn matmul() metodia --> np.matmul(A1, B1) )
[[121 188]
[ 71 108]
[ 25 37]]
Lopputuloksena m x n ja n x p matriisien kertolaskusta tulee m x p muotoinen matriisi (yllä C1 = 3 x 2)
#Tarkistetaan vielä matriisin C1 muoto
shape(C1)
(3, 2)
A1*B1 #Huomataan, että "tavallinen kertolasku" ei toimi, koska matriisit eivät ole samanmuotoiset.
#Muutenkin tavallisen kertomerkin käyttäminen tuottaisi lopputulokseksi ns. Hadamard tulon, jota ei juuri käytetä.
#Hadamard-tulon voi laskea vain samanmuotoisille matriiseille.
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-128-7c9a111d8157> in <module>()
----> 1 A1*B1 #Huomataan, että "tavallinen kertolasku" ei toimi, koska matriisit eivät ole samanmuotoiset. Muutenkin tavallisen
ValueError: operands could not be broadcast together with shapes (3,4) (4,2)
B1.dot(A1)
#Väärän muotoisten matriisien kertolaskusta tulee error
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-129-d3a8b6b19347> in <module>()
----> 1 B1.dot(A1)
2 #Väärän muotoisten matriisien kertolaskusta tulee error
ValueError: shapes (4,2) and (3,4) not aligned: 2 (dim 1) != 3 (dim 0)
A = array([[2,4],
[1,3]])
B= array([[0,5],
[2,9]])
#Edellä muodostetut matriisit A ja B ovat 2 x 2 matriiseja. Näin ollen sarakkeiden ja rivien määrä täsmää,
# ja ne voidaan kertoa keskenään kummin päin tahansa, mutta lopputulokset EIVÄT OLE SAMAT.
C = A.dot(B)
print(C)
[[ 8 46]
[ 6 32]]
D = B.dot(A)
print(D)
[[ 5 15]
[13 35]]
D == C
array([[False, False],
[False, False]], dtype=bool)
Erityisiä matriiseja
Sarakkeiltaan ja riveiltään identtinen matriisi on neliömatriisi. Yllä A & B ovat neliömatriiseja.
Matriiseja, joiden kaikki alkiot ovat nollia, eli jotka ovat muotoa 0 m*n, ovat nollamatriiseja
Z= np.zeros((5,5))
#Numpyn zeros() metodilla saadaan haluttu nollamatriisi
print(Z)
[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
Ns. identiteettimatriiseja puolestaan ovat matriisit, joiden lävistäjäalkiot ovat ykkösiä, ja kaikki muut nollia.
I = np.eye(5)
print(I)
[[ 1. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. 0. 1. 0.]
[ 0. 0. 0. 0. 1.]]
Nollamatriisi voi olla mitä tahansa tyyppiä. Sen sijaan ykkösmatriisissa on aina yhtä paljon rivejä ja sarakkeita.
#Huom! Identiteettimatriisista käytetään paikoin myös nimeä yksikkömatriisia.
#Numpyn metodeista löytyy myös ones() metodi. Tämä tuottaa siis matriisin, jonka kaikki alkiot ovat ykkösiä
O = np.ones((5,5))
print(O)
[[ 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1.]]
Jos identiteettimatriisin kertoo reaaliluvulla, mitä tulee tulokseksi?
Matriisi, jonka kaikki nollasta poikkeavat alkiot ovat lävistäjällä, on lävistäjämatriisi. Lävistäjämatriisi, jonka kaikki lävistäjäalkiot ovat samoja, on puolestaan skalaarimatriisi. Skalaarimatriisit ovat identiteettimatriisin skalaarimonikertoja.
Jos identiteettimatriisilla kertoo sopivan muotoisen, ns. normaalin matriisin A, niin mitä tulee tulokseksi?
Matriisin kertominen vektorilla
Matriisin ja vektorin kertolaskun voi ajatella olevan kuin matriisin kertomisen yksisarakkeisella matriisilla.
Esim. jos on meillä on matriisi O (np.ones((5,5)), joka on siis muotoa 5 x 5, ja vektori y ( array([[2],[3],[4],[5],[6]])), joka on siis muodoltaan 5 x 1 matriisi.
y= array([[2],[3],[4],[5],[6]])
type(y)
numpy.ndarray
Missä järjestyksessä matriisi O ja vektori y tulee nyt kertoa?
Matriisien laskusäännöistä

Matriisin transpoosi
Matriisin voi kääntää, eli ns. transponoida. Tällöin matriisin rivit ja sarakkeet vaihtavat paikkaa.
#Muodostetaan ensin matriisi R, ja tarkistetaan R:n muoto
R = range(20)
R = np.reshape(R,(4,5))
print(R)
shape(R)
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]
[15 16 17 18 19]]
(4, 5)
#Transponoidaan R ja tarkistetaan R:n muoto uudelleen
S= R.T
print('S')
print(S)
shape(S)
S
[[ 0 5 10 15]
[ 1 6 11 16]
[ 2 7 12 17]
[ 3 8 13 18]
[ 4 9 14 19]]
(5, 4)