Pääkomponenttianalyysi (PCA)
Voit ladata tehtävät tästä. Voit myös ladata tämän materiaalin muistiona tästä.
Yleiskatsaus teoriaan
Pääkomponenttianalyysi on menetelmä, jossa moniulotteiselle datasetille määritellään uudet muuttujat, jotka ovat lineaarisia yhdistelmiä alkuperäisistä muuttujista. Tyypillisesti pääkomponenttianalyysia käytetään kun muuttujia on paljon ja/tai jotkin muuttujat korreloivat vahvasti keskenään. Tällöin PCA:n avulla muuttujien määrää saadaan pienemmäksi esimerkiksi visualisointia varten, ja multikollineariteetin aiheuttamista ongelmista päästään kätevästi eroon. Yksinkertaistettuna, PCA on tapa tiivistää dataa ja selittää ilmiötä pienemmällä määrällä muuttujia kuin alkuperäisessä datasetissä. PCA:n tuloksena on siis lista pääkomponentteja, joiden avulla datasettiä voidaan kuvailla säilyttäen mahdollisimman paljon alkuperäisestä informaatiosta.
- Komponenttien varianssia kuvataan ominaisarvolla (eigenvalue, characteristic root, latent root)
- Pääkomponentit valitaan siten, että ne eivät korreloi keskenään
- Pääkomponentit ovat keskenään ortogonaalisia, eli suorakulmassa keskenään. Niitä voidaan valita maksimissaan alkuperäisen muuttujien määrän verran.
Pääkomponenttianalyysi on vaiheittainen:
- Ensimmäinen pääkomponnetti selittää suurimman osan datan vaihtelusta
- Datan vaihtelu eliminoidaan tämän komponentin suunnassa. Seuraavaksi valitaan toinen pääkomponentti, joka selittää jäljelle jääneen datan vaihtelusta suurimman osan
- Viimeisillä pääkomponenteilla on jo niin pieni varianssi, että ne voidaan kokonaan jättää pois. Tähän perustuu vektoreiden tiivistäminen (dimension alentaminen).
Viiniesimerkki
Otetaan havainnollistukseksi vaikkapa täältä löytynyt hauska ja havainnollistava tapa selittää PCA:ta - viiniesimerkki (kaikki kunnia alkuperäiselle kirjoittajalle). Erilaisia viinejä on mahdollista kuvailla mm. niiden hajun, värin, erilaisten aromien, iän, tanniinisuuden, ja vaikka kuinka monen muun ominaisuuden avulla. Kuitenkin monet näistä ominaisuuksista liittyvät jollain tapaa toisiinsa, joten itseasiassa meidän onkin mahdollista kuvailla viiniä paljon pienemmällä määrällä ominaisuuksia - juuri näin PCA toimii. Alkuperäisten ominaisuuksien joukosta ei tosin valita tiettyjä, tärkeimpiä ominaisuuksia, vaan niistä yhdistellään kokonaan uusia, keskenään korreloimattomia ominaisuuksia.
Eräs uusi viiniä kuvaileva muuttuja saattaisi olla vaikkapa seuraava vähennyslasku: (viinin ikä - viinin happoisuus). Näitä syntyviä yhdistelmiä kutsutaan lineaarikombinaatioiksi. Voi olla kuitenkin vaikeaa tietää, mitkä yhdistelmät kaikista ominaisuuksista kuvailevat viiniä kaikista parhaiten - tässä piileekin PCA:n hienous. PCA:n avulla on nimittäin mahdollista löytää ja valita juuri kaikista parhaiten viinin ominaisuuksia summaavat kombinaatiot alkuperäisistä muuttujista.
Mutta mitä itseasiassa viinin ominaisuuksien selittäminen tai niiden summaaminen edes tarkoittaa tässä kontekstissa? Minkälainen muuttuja on hyvä tähän tarkoitukseen? Voidaan ajatella kahta asiaa:
- Sellaiset ominaisuudet, jotka erottavat eri viinit toisistaan. Jos ajatellaan vaikkapa punaista väriä, joka on sama melkeinpä kaikille punaviineille, ei tällainen muuttuja olisi kovinkaan hyödyllinen viinien kuvailemiseen. Etsitään siis sellaisia muuttujia, joilla on paljon vaihtelua eri viinien kesken.
- Sellaiset ominaisuudet, joiden perusteella saadaan uudelleen johdettua alkuperäiset ominaisuudet. Jos otetaan sellainen muuttuja, jolla ei ole mitään tekemistä alkuperäisten ominaisuuksien kanssa, tämä olisi jälleen hieman hyödytön viinien ominaisuuksien summaamisen kannalta. Halutaan siis löytää sellaisia muuttujia, joiden perusteella alkuperäiset ominaisuudet ovat mahdollisimman hyvin rekonstruoitavissa. Itseasiassa, nämä kaksi tavoitetta ovatkin keskenään ekvivalentteja, ja PCA:n avulla pyritään juuri saavuttamaan nämä molemmat.
Mutta miten ihmeessä nämä voivat olla keskenään ekvivalentteja? Kuvitellaan kaksi muuttujaa $x$ ja $y$, jotka korreloivat keskenään. Niistä piirretty kuvaaja voisi näyttää vaikkapa seuraavalta:
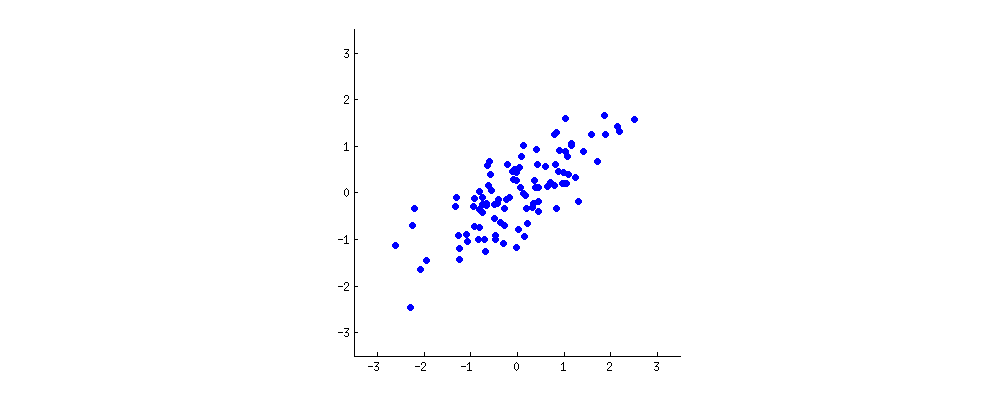
Uusi muuttuja voidaan rakentaa piirtämällä suora pisteiden keskelle, ja projektoimalla kaikki pisteet tälle suoralle. Jokainen syntyvä suora vastaa lineaarikombinaatiota $c_1 x + c_2 y$, missä $c_1$ ja $c_2$ vastaavat tiettyjä vakioita (kertoimia).
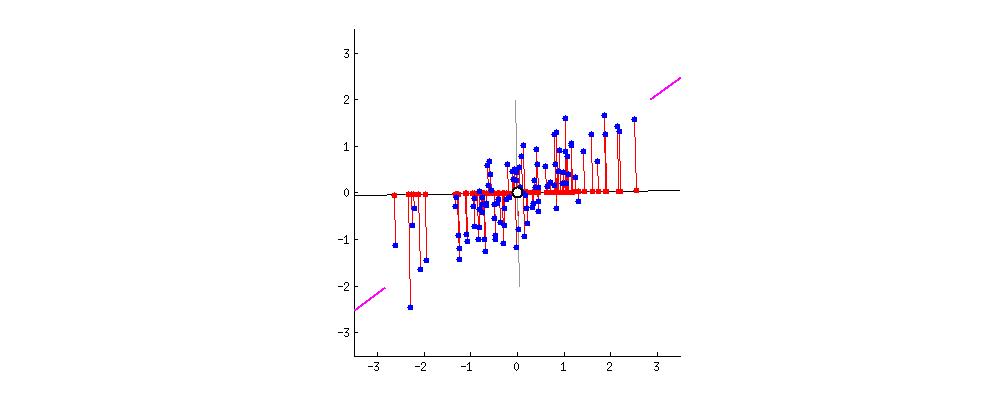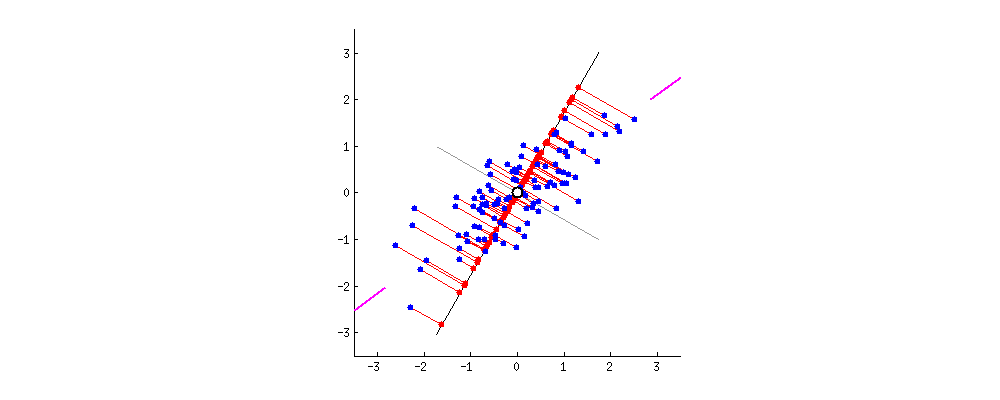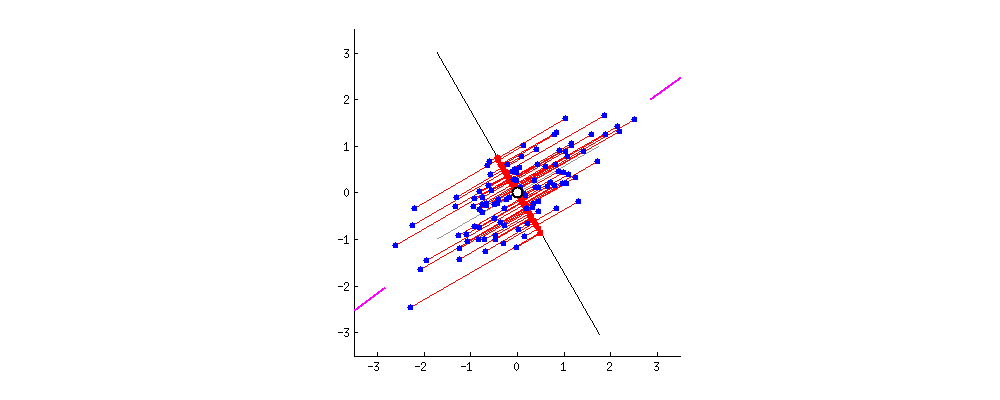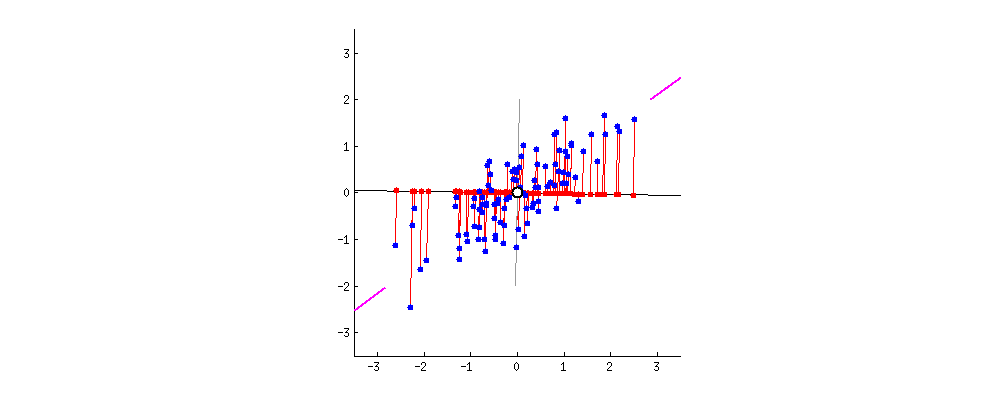
Huomaamme tuijottamalla kuvaa hetken aikaa, että suoralle asettuvien punaisten pisteiden etäisyys (varianssi) saavuttaa maksimin samalla hetkellä kuin punaisten viivojen pituus ( pienimmän neliösumman virhe (MSE) ) saavuttaa minimin. Tällä suoralla (tai akselilla) onkin ensimmäinen pääkomponenttimme, joka siis löytyi maksimoimalla varianssia tai minimoimalla virhettä.
Lineaarikombinaatio
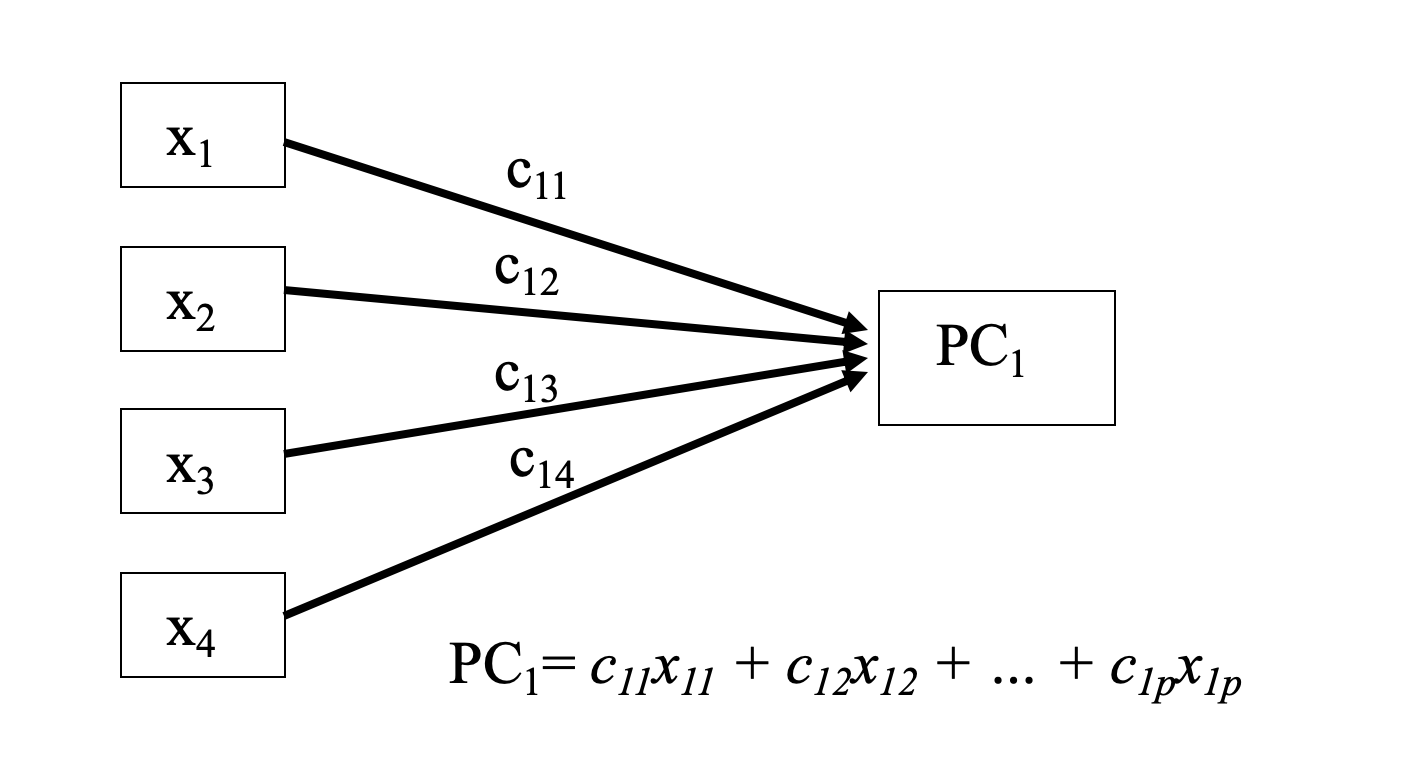Kuvassa alkuperäisisten komponenttien $x_i$ lineaarikombinaatio muodostaa pääkomponentin $PC_1$. Lähde: Tampereen yliopiston luentomateriaalit
Esimerkki: Yritysjohtajien palkkadata
Muistellaan Lineaarisessa Regressiossa käytettyä datasettiä yritysjohtajien palkoista. Käytetään jälleen samaa dataa tässä workshopissa, sillä tällöin totesimme datassa olevan keskenään korreloivia muuttujia, ja muistamme niiden myös aiheuttaneen hieman hankaluuksia regressiomallillemme.
# Aloitetaan tuttuun tyyliin kirjastojen tuonnilla, ja käytetään Pandas- sekä Numpy-kirjastoja kuten aiemminkin
%matplotlib inline
import pandas as pd
import numpy as np
# Desimaalit on eroteltu pilkulla ja solut puolipisteellä
# jos datasettisi on samassa kansiossa, tämän pitäisi toimia suoraan. Jos datasetti on eri kansiossa,
# lisää alkuun kansion polku, esim '../data/ceosal2.csv'
df = pd.read_csv('ceosal2.csv', sep = ';', decimal = ',')
# tulostetaan datasetin viimeiset rivit
df.tail()
| salary | age | college | grad | comten | ceoten | sales | profits | mktval | lsalary | lsales | lmktval | comtensq | ceotensq | profmarg | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 172 | 264 | 63 | 1 | 0 | 42 | 3 | 334 | 43 | 480 | 5.575949 | 5.811141 | 6.173786 | 1764 | 9 | 12.874250 |
| 173 | 185 | 58 | 1 | 0 | 39 | 1 | 766 | 49 | 560 | 5.220356 | 6.641182 | 6.327937 | 1521 | 1 | 6.396867 |
| 174 | 387 | 71 | 1 | 1 | 32 | 13 | 432 | 28 | 477 | 5.958425 | 6.068426 | 6.167517 | 1024 | 169 | 6.481482 |
| 175 | 2220 | 63 | 1 | 1 | 18 | 18 | 277 | -80 | 540 | 7.705263 | 5.624018 | 6.291569 | 324 | 324 | -28.880870 |
| 176 | 445 | 69 | 1 | 0 | 23 | 0 | 249 | 31 | 828 | 6.098074 | 5.517453 | 6.719013 | 529 | 0 | 12.449800 |
# Tulostetaan vielä datasetin muoto, jotta meillä on hyvä kuva siitä, millaisen datan kanssa olemme tekemisissä
df.shape
(177, 15)
# Seuraavaksi haluamme piirrellä datasta hieman kuvaajia, joten jatketaan siihen tarvittavien kirjastojen tuonnilla
import seaborn as sns; sns.set()
import matplotlib.pyplot as plt
Jatketaan tällä kertaa vain tasomuuttujien kanssa, sillä muistelemme, että tasomuuttujien tapauksessa multikollineariteetti vaikutti olevan suurempi ongelma kuin log-muuttujien kanssa. Piirretään parittaiset kuvat kaikista muista, paitsi neliömuotoisista muuttujista. Tällä kertaa emme myöskään poista muuttujaa “college”, vaikka viimeksi totesimme havaintoja olevan liian vähän, jotta muuttujaa kannattaisi ottaa mukaan malliin. Palataan tähän aiheeseen hieman myöhemmin.
df_taso = df.drop(['lsalary', 'lsales', 'lmktval'], axis = 1)
df_taso.shape
(177, 12)
# jätetään neliömuotoiset muuttujat pois
sns.pairplot(df_taso.drop(['comtensq', 'ceotensq'], axis = 1))
plt.show()
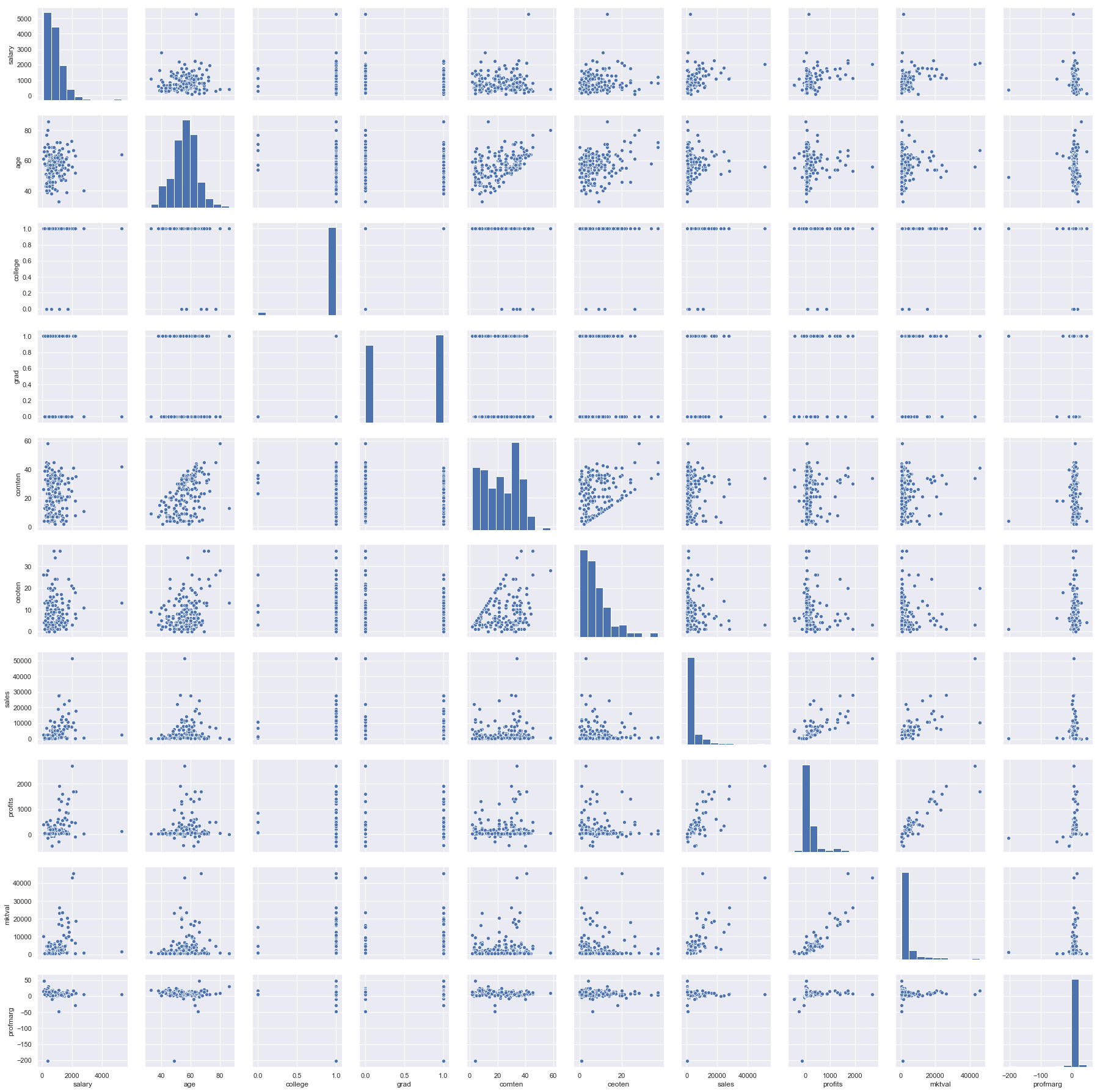
Kuten muistelimme, kuvaajista huomataan, että joidenkin muuttujien välillä näyttäisi olevan korrelaatioita. Lasketaan vielä korrelaatiomatriisi asian varmistamiseksi ja piirretään kuva asian havainnollistamiseksi
corr = df_taso.drop(['comtensq', 'ceotensq'], axis = 1).corr()
corr
| salary | age | college | grad | comten | ceoten | sales | profits | mktval | profmarg | |
|---|---|---|---|---|---|---|---|---|---|---|
| salary | 1.000000 | 0.115384 | -0.067025 | -0.003000 | 0.037698 | 0.142948 | 0.380224 | 0.393928 | 0.406307 | -0.028935 |
| age | 0.115384 | 1.000000 | -0.178062 | -0.123163 | 0.479414 | 0.338742 | 0.127134 | 0.114743 | 0.107179 | 0.014678 |
| college | -0.067025 | -0.178062 | 1.000000 | 0.181445 | -0.157109 | -0.106288 | -0.021492 | -0.045982 | -0.027578 | -0.017531 |
| grad | -0.003000 | -0.123163 | 0.181445 | 1.000000 | -0.228335 | -0.102806 | 0.076326 | 0.097826 | 0.122976 | -0.015395 |
| comten | 0.037698 | 0.479414 | -0.157109 | -0.228335 | 1.000000 | 0.315121 | 0.104400 | 0.143737 | 0.136096 | 0.047174 |
| ceoten | 0.142948 | 0.338742 | -0.106288 | -0.102806 | 0.315121 | 1.000000 | -0.067715 | -0.021607 | 0.006609 | 0.048805 |
| sales | 0.380224 | 0.127134 | -0.021492 | 0.076326 | 0.104400 | -0.067715 | 1.000000 | 0.798287 | 0.754662 | -0.017353 |
| profits | 0.393928 | 0.114743 | -0.045982 | 0.097826 | 0.143737 | -0.021607 | 0.798287 | 1.000000 | 0.918128 | 0.125479 |
| mktval | 0.406307 | 0.107179 | -0.027578 | 0.122976 | 0.136096 | 0.006609 | 0.754662 | 0.918128 | 1.000000 | 0.067019 |
| profmarg | -0.028935 | 0.014678 | -0.017531 | -0.015395 | 0.047174 | 0.048805 | -0.017353 | 0.125479 | 0.067019 | 1.000000 |
sns.heatmap(corr)
plt.xticks(range(len(corr.columns)), corr.columns)
plt.yticks(range(len(corr.columns)), corr.columns)
plt.show()
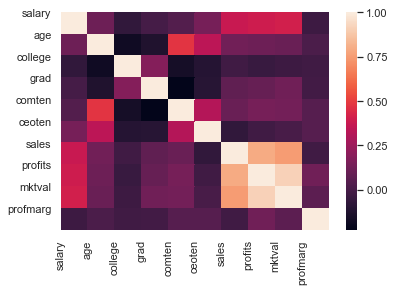
Tosiaan, etenkin yrityksen voiton ja markkina-arvon välillä oli todella iso korrelaatio. Katsotaan seuraavaksi mitä voimme tehdä asialle PCA:n avulla.
Vielä pari sanaa muuttujista: PCA:n käyttämisestä kategoriseen dataan on ollut paljon keskustelua, ja hieman eriäviä mielipiteitä jopa alan ammattilaisten keskuudessa. Yleisesti “hyväksyttyä” on kuitenkin soveltaa PCA:ta dataan, jossa kategoriset muuttujat ovat binäärisiä (0 tai 1). Koska PCA:ssa on pohjimmiltaan kyse varianssin maksimoinnista ja ominaisarvoista, kategorinen data on hieman kinkkinen tässä yhteydessä. Pidetään kuitenkin demonstraation vuoksi binääriset muuttujat “college” ja “grad” mukana seuraavassa muunnoksessa.
# Koska suuresti poikkeavat havainnot (outlierit) vääristävät myös PCA:n tulosta,
# poistetaan vielä poikkeavat havainnot, kuten viimeksi.
df_taso = df_taso[df_taso.salary < 5000]
# Jaetaan lisäksi data kahteen eri osaan (selittäviin ja selitettävään muuttujiin)
X = df_taso.drop(['salary'], axis = 1)
y = df_taso.salary
PCA vaihe vaiheelta
X.shape
(176, 11)
# Muunnetaan DataFrame numpy array-muotoon
Data_matrix = np.array(X)
print(Data_matrix)
[[ 4.900000e+01 1.000000e+00 1.000000e+00 ... 8.100000e+01
4.000000e+00 1.558065e+01]
[ 4.300000e+01 1.000000e+00 1.000000e+00 ... 1.000000e+02
1.000000e+02 1.696113e+01]
[ 5.100000e+01 1.000000e+00 1.000000e+00 ... 8.100000e+01
9.000000e+00 2.366864e+01]
...
[ 7.100000e+01 1.000000e+00 1.000000e+00 ... 1.024000e+03
1.690000e+02 6.481482e+00]
[ 6.300000e+01 1.000000e+00 1.000000e+00 ... 3.240000e+02
3.240000e+02 -2.888087e+01]
[ 6.900000e+01 1.000000e+00 0.000000e+00 ... 5.290000e+02
0.000000e+00 1.244980e+01]]
# Lasketaan jokaisen sarakkeen keskiarvo
Columns_mean = np.mean(Data_matrix.T, axis=1)
print(Columns_mean)
[5.63863636e+01 9.71590909e-01 5.34090909e-01 2.23920455e+01
7.92613636e+00 3.53588068e+03 2.08335227e+02 3.61225000e+03
6.50392045e+02 1.13812500e+02 6.42841609e+00]
# Vähennetään jokaisesta sarakkeesta (sarakkeen jokaisesta alkiosta) äsken laskettu keskiarvo
Zero_mean_cols = Data_matrix - Columns_mean
print(Zero_mean_cols)
[[-7.38636364e+00 2.84090909e-02 4.65909091e-01 ... -5.69392045e+02
-1.09812500e+02 9.15223391e+00]
[-1.33863636e+01 2.84090909e-02 4.65909091e-01 ... -5.50392045e+02
-1.38125000e+01 1.05327139e+01]
[-5.38636364e+00 2.84090909e-02 4.65909091e-01 ... -5.69392045e+02
-1.04812500e+02 1.72402239e+01]
...
[ 1.46136364e+01 2.84090909e-02 4.65909091e-01 ... 3.73607955e+02
5.51875000e+01 5.30659125e-02]
[ 6.61363636e+00 2.84090909e-02 4.65909091e-01 ... -3.26392045e+02
2.10187500e+02 -3.53092861e+01]
[ 1.26136364e+01 2.84090909e-02 -5.34090909e-01 ... -1.21392045e+02
-1.13812500e+02 6.02138391e+00]]
# Lasketaan saadulle matriisille kovarianssimatriisi
V = np.cov(Zero_mean_cols.T)
print(V)
[[ 7.10041558e+01 -2.51818182e-01 -4.98961039e-01 4.90762338e+01
2.02972727e+01 6.60556636e+03 3.96944026e+02 5.93974286e+03
2.46081338e+03 5.91427143e+02 2.28408350e+00]
[-2.51818182e-01 2.77597403e-02 1.52597403e-02 -3.25941558e-01
-1.27824675e-01 -2.16834091e+01 -3.09327922e+00 -2.93471429e+01
-1.55145130e+01 -2.77107143e+00 -5.20844889e-02]
[-4.98961039e-01 1.52597403e-02 2.50259740e-01 -1.35344156e+00
-3.54610390e-01 2.30452662e+02 1.96427922e+01 3.92334286e+02
-6.70791558e+01 -1.27050000e+01 -1.42856128e-01]
[ 4.90762338e+01 -3.25941558e-01 -1.35344156e+00 1.49839708e+02
2.72976948e+01 7.98641276e+03 7.28793539e+02 1.10765586e+04
6.76325685e+03 8.47056786e+02 1.05820408e+01]
[ 2.02972727e+01 -1.27824675e-01 -3.54610390e-01 2.72976948e+01
5.12802273e+01 -2.93232315e+03 -6.02722403e+01 3.67115714e+02
1.31909198e+03 1.41785464e+03 6.31128920e+00]
[ 6.60556636e+03 -2.16834091e+01 2.30452662e+02 7.98641276e+03
-2.93232315e+03 3.72762172e+07 1.97650489e+06 2.97569619e+07
3.39784790e+05 -7.72913768e+04 -1.90742725e+03]
[ 3.96944026e+02 -3.09327922e+00 1.96427922e+01 7.28793539e+02
-6.02722403e+01 1.97650489e+06 1.64472693e+05 2.40487791e+06
3.18980735e+04 -8.46953929e+02 9.10877249e+02]
[ 5.93974286e+03 -2.93471429e+01 3.92334286e+02 1.10765586e+04
3.67115714e+02 2.97569619e+07 2.40487791e+06 4.17147290e+07
4.92012353e+05 1.44504700e+04 7.73785664e+03]
[ 2.46081338e+03 -1.55145130e+01 -6.70791558e+01 6.76325685e+03
1.31909198e+03 3.39784790e+05 3.18980735e+04 4.92012353e+05
3.27927440e+05 4.32855939e+04 3.87651602e+02]
[ 5.91427143e+02 -2.77107143e+00 -1.27050000e+01 8.47056786e+02
1.41785464e+03 -7.72913768e+04 -8.46953929e+02 1.44504700e+04
4.32855939e+04 4.54251932e+04 8.17569560e+01]
[ 2.28408350e+00 -5.20844889e-02 -1.42856128e-01 1.05820408e+01
6.31128920e+00 -1.90742725e+03 9.10877249e+02 7.73785664e+03
3.87651602e+02 8.17569560e+01 3.20816735e+02]]
# Ratkaistaan kovarianssimatriisin ominaisarvot ja ominaisvektorit
from numpy.linalg import eig
values, vectors = eig(V)
# Tulostetaan ensimmäiset 7 ominaisvektoria:
print('Vektorit:', vectors.T[0:7])
Vektorit: [[-1.27755868e-04 5.25241712e-07 -6.39320039e-06 -1.96141511e-04
2.46962049e-05 -6.79484942e-01 -4.47854133e-02 -7.32270873e-01
-8.56913788e-03 5.99179536e-04 -6.35328316e-05]
[ 8.02837064e-05 4.40337220e-07 -1.00575126e-05 -1.81041012e-04
-2.50609283e-04 7.33488697e-01 -1.94013866e-02 -6.79326259e-01
-9.20729933e-03 -6.95675522e-03 -6.91212447e-04]
[ 7.47082094e-03 -4.69209576e-05 -2.21962380e-04 2.03312546e-02
4.58320516e-03 1.55567340e-03 1.11927876e-02 -1.35772256e-02
9.88292761e-01 1.49914400e-01 9.06618434e-04]
[ 6.17037368e-03 -1.04562056e-05 -5.54956477e-05 -4.18970604e-03
3.09006451e-02 6.07819385e-03 -4.76406762e-02 -1.70240795e-04
-1.49310493e-01 9.87111203e-01 -8.73031914e-04]
[ 8.08979591e-05 5.71139181e-05 6.65341558e-05 -9.79199225e-05
-4.43585198e-04 1.59474565e-02 -9.97231162e-01 4.59374909e-02
1.88130921e-02 -4.53849745e-02 -2.74132382e-02]
[-1.21305402e-03 1.37965333e-06 4.47976068e-04 -7.83804473e-03
-1.42527858e-02 -9.05016543e-04 2.74020191e-02 -7.54826114e-04
6.87317704e-04 9.68433220e-04 -9.99489911e-01]
[-9.98194705e-01 2.62422984e-03 -2.31185308e-04 3.50161220e-02
-4.75664454e-02 1.96455109e-04 -3.96001156e-04 -5.48942648e-05
5.72452545e-03 8.72430966e-03 1.61648102e-03]]
# Lasketaan uudet muuttujat projektoimalla
P = vectors.T[0:7].dot(Zero_mean_cols.T)
print(P.T)
print('Uusia sarakkeita', len(P))
print('Havaintoja', len(P[0]))
[[-1.61828838e+04 -1.13610678e+04 -8.32857358e+02 ... 1.80755389e+02
-5.88153728e+00 2.13128915e+00]
[ 4.06182325e+03 -6.71046015e+02 -5.19097803e+02 ... -1.74075387e+01
-1.03882800e+01 9.13774060e+00]
[ 4.13974968e+03 -7.53702571e+02 -5.51771031e+02 ... -7.65513989e+00
-1.72116962e+01 5.39068484e-01]
...
[ 4.40979676e+03 -1.47130716e+02 4.13556071e+02 ... -9.16800617e+00
3.26133885e-01 -1.22381661e+01]
[ 4.47991810e+03 -2.96131774e+02 -2.57670993e+02 ... 7.97192323e+01
3.25209113e+01 -7.68386954e+00]
[ 4.28112287e+03 -5.14126953e+02 -1.06252967e+02 ... -7.53636157e-01
-5.90234035e+00 -1.42931347e+01]]
Uusia sarakkeita 7
Havaintoja 176
Näin saimme laskettua uudet pääkomponentit datasetillemme ja vähensimme samalla sarakkeiden määrää 11 -> 7. Oikeasti ei tietenkään joka kerta tarvitse laskea tätä kaikkea alusta alkaen. Turvaudumme jälleen scikit-learn kirjastoon, josta löytyy valmiina PCA. Toistetaan nyt sama homma kirjaston avulla.
PCA scikit-learnin avulla
# Käytetään taas tuttua scikit-learn kirjastoa, ja tuodaan sieltä PCA
from sklearn.decomposition import PCA
X.shape
(176, 11)
Valitaan sattumanvaraisesti uusien muuttujien lukumääräksi 7
# Sovitetaan pca datasettiin X
pca = PCA(n_components=7)
df_pca = pca.fit(X)
df_pca
PCA(copy=True, iterated_power='auto', n_components=7, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
# Tulostetaan vielä syntyneet uudet pääkomponenttivektorit (kertoimet), ja varmistetaan että niitä oli seitsemän
print(pca.components_)
print('Komponenttien määrä:', len(pca.components_))
[[ 1.27755868e-04 -5.25241712e-07 6.39320039e-06 1.96141511e-04
-2.46962049e-05 6.79484942e-01 4.47854133e-02 7.32270873e-01
8.56913788e-03 -5.99179536e-04 6.35328316e-05]
[-8.02837064e-05 -4.40337220e-07 1.00575126e-05 1.81041012e-04
2.50609283e-04 -7.33488697e-01 1.94013866e-02 6.79326259e-01
9.20729933e-03 6.95675522e-03 6.91212447e-04]
[ 7.47082094e-03 -4.69209576e-05 -2.21962380e-04 2.03312546e-02
4.58320516e-03 1.55567340e-03 1.11927876e-02 -1.35772256e-02
9.88292761e-01 1.49914400e-01 9.06618434e-04]
[ 6.17037368e-03 -1.04562056e-05 -5.54956477e-05 -4.18970604e-03
3.09006451e-02 6.07819385e-03 -4.76406762e-02 -1.70240795e-04
-1.49310493e-01 9.87111203e-01 -8.73031914e-04]
[ 8.08979591e-05 5.71139181e-05 6.65341558e-05 -9.79199225e-05
-4.43585198e-04 1.59474565e-02 -9.97231162e-01 4.59374909e-02
1.88130921e-02 -4.53849745e-02 -2.74132382e-02]
[-1.21305402e-03 1.37965333e-06 4.47976068e-04 -7.83804473e-03
-1.42527858e-02 -9.05016543e-04 2.74020191e-02 -7.54826114e-04
6.87317704e-04 9.68433220e-04 -9.99489911e-01]
[ 9.98194705e-01 -2.62422984e-03 2.31185308e-04 -3.50161220e-02
4.75664454e-02 -1.96455109e-04 3.96001156e-04 5.48942648e-05
-5.72452545e-03 -8.72430966e-03 -1.61648102e-03]]
Komponenttien määrä: 7
Huomaamme nyt, että saadut vektorit ovat etumerkkiä lukuunottamatta samat kuin aikaisemmin manuaalisesti lasketut ominaisvektorit. Itseasiassa onkin juuri niin, että ominaisarvot ovat yksikäsitteisiä, mutta ominaisvektorit eivät ole. Jokainen ominasvektori voidaan kertoa skalaarilla, ja silti kyseessä on edelleen ominaisvektori.
# Tulostetaan lisäksi tieto siitä, kuinka paljon varianssista kukin pääkomponenteista selittää.
# Huomamme, että ensimmäinen pääkomponentti selittää suurimman osan datan varianssista, ja jokainen
# seuraava hieman vähemmän kuin edeltäjänsä
print(pca.explained_variance_)
[6.94794847e+07 9.66076478e+06 3.28794487e+05 3.84846848e+04
2.14688965e+04 2.99790731e+02 5.01491379e+01]
# Seuraavaksi lasketaan datasetin X muunnos uusien pääkomponenttien suuntaan
data_pca = pca.transform(X)
# Varmistetaan, että datasetin havaintojen määrä pysyi ennallaan,
# ja uusien komponenttien määrä oli muunnoksen jälkeen haluttu 7
data_pca.shape
(176, 7)
# Tehdään muunnoksen tuloksesta DataFrame ja nimetään sarakkeet vielä pääkomponenttien mukaan
df_pca = pd.DataFrame(data=data_pca, columns=['PC1', 'PC2', 'PC3', 'PC4', 'PC5', 'PC6', 'PC7'])
df_pca.head()
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | |
|---|---|---|---|---|---|---|---|
| 0 | 16182.883841 | 11361.067783 | -832.857358 | -46.798810 | 180.755389 | -5.881537 | -2.131289 |
| 1 | -4061.823251 | 671.046015 | -519.097803 | 56.863543 | -17.407539 | -10.388280 | -9.137741 |
| 2 | -4139.749681 | 753.702571 | -551.771031 | -30.607073 | -7.655140 | -17.211696 | -0.539068 |
| 3 | -3581.416594 | 8.070269 | -80.170193 | 388.834998 | 83.135700 | 8.367577 | -2.728417 |
| 4 | -4538.893994 | 135.636784 | -554.768042 | 0.449907 | -26.656223 | -1.495580 | -7.541237 |
# Lasketaan uusi korrelaatiomatriisi eri pääkomponenttien kesken
corr = df_pca.corr()
corr
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | |
|---|---|---|---|---|---|---|---|
| PC1 | 1.000000e+00 | -2.696046e-16 | -2.741667e-15 | -1.373417e-15 | -1.213021e-15 | -7.671728e-14 | 8.809378e-15 |
| PC2 | -2.696046e-16 | 1.000000e+00 | 3.233909e-14 | -3.900986e-16 | -2.339383e-16 | -8.220617e-15 | -6.184811e-15 |
| PC3 | -2.741667e-15 | 3.233909e-14 | 1.000000e+00 | 3.229484e-16 | -1.374511e-16 | -1.691589e-15 | 1.271877e-15 |
| PC4 | -1.373417e-15 | -3.900986e-16 | 3.229484e-16 | 1.000000e+00 | 3.731388e-17 | 3.863407e-17 | 7.453920e-16 |
| PC5 | -1.213021e-15 | -2.339383e-16 | -1.374511e-16 | 3.731388e-17 | 1.000000e+00 | 6.029777e-15 | -2.284929e-16 |
| PC6 | -7.671728e-14 | -8.220617e-15 | -1.691589e-15 | 3.863407e-17 | 6.029777e-15 | 1.000000e+00 | 1.417278e-16 |
| PC7 | 8.809378e-15 | -6.184811e-15 | 1.271877e-15 | 7.453920e-16 | -2.284929e-16 | 1.417278e-16 | 1.000000e+00 |
# Tarkastellan korrelaatioita vielä visualisoinnin avulla. Huomaamme, että nyt syntyneet muuttujat
# eivät enää korreloi keskenään, eli pääsimme eroon multikollineariteetista.
sns.heatmap(corr)
plt.xticks(range(len(corr.columns)), corr.columns)
plt.yticks(range(len(corr.columns)), corr.columns)
plt.show()
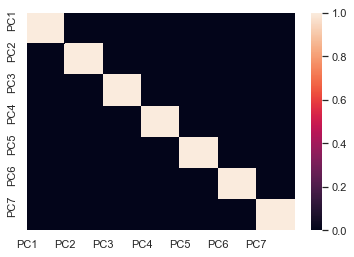
Tämän muunnoksen jälkeen uutta datasettiä voisi käyttää vaikkapa lineaarisessa regressiossa, kuten alkuperäistäkin datasettiä käytettiin. Ei kuitenkaan mennä regressioon tällä kertaa, vaan jatketaan PCA:n kanssa.
Pääkomponenttien määrän valitseminen
Tulostetaan vielä kuvaaja selitetystä varianssista eri komponenttien määrille. Huomaamme, että jo ensimmäinen komponentti selittää suurimman osan varianssista, ja selitysaste ei oikeastaan juurikaan parane lisäämällä muita komponentteja. Itse asiassa ensimmäiset kaksi komponenttia selittävät jo 100% varianssista. Olisimme voineet siis supistaa datan kahteen dimensioon menettämättä käytännössä yhtään informaatiota verrattuna vaikkapa seitsemään komponenttiin. Tällä tekniikalla voidaan tutkia sopivaa komponenttimäärää kätevästi.
pca = PCA().fit(X)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance')
Text(0,0.5,'cumulative explained variance')
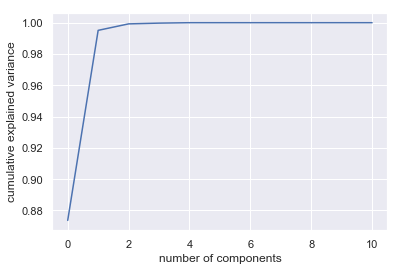
Tehdään sama temppu vielä siten, että säilytämme ainoastaan kaksi dimensiota.
# Lyhennetty tapa valita säilytettäväksi kaksi pääkomponenttia
pca = PCA(2).fit(X)
print(pca)
PCA(copy=True, iterated_power='auto', n_components=2, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
Tulostetaan muunnoksen tuottamat komponentit. Huomataan, että pääkomponenttivektoreita on kaksi (kuten pitikin), ja niiden pituus on 11, sillä alkuperäisiä muuttujia (sarakkeita) oli 11. Jokainen alkuperäinen havainto (jolla on 11 ulottuvuutta) muunnetaan kaksiulotteiseksi pääkomponenttivektoreiden alkioiden eli kertoimien avulla.
print(pca.components_)
[[ 1.27755868e-04 -5.25241712e-07 6.39320039e-06 1.96141511e-04
-2.46962049e-05 6.79484942e-01 4.47854133e-02 7.32270873e-01
8.56913788e-03 -5.99179536e-04 6.35328316e-05]
[-8.02837064e-05 -4.40337220e-07 1.00575126e-05 1.81041012e-04
2.50609283e-04 -7.33488697e-01 1.94013866e-02 6.79326259e-01
9.20729933e-03 6.95675522e-03 6.91212447e-04]]
Muunnoksen jälkeen siis uudet datapisteet ovat kaksiulotteisia:
test = pca.transform(X)
print(test[:5])
[[ 1.61828838e+04 1.13610678e+04]
[-4.06182325e+03 6.71046015e+02]
[-4.13974968e+03 7.53702571e+02]
[-3.58141659e+03 8.07026854e+00]
[-4.53889399e+03 1.35636784e+02]]
Toisinsanottuna pääkomponentteja on muunnoksen jälkeen kaksi. Nimetään ne uuteen dataframeen nimillä PC1 ja PC2:
df_pca = pd.DataFrame(test, columns=['PC1', 'PC2'])
df_pca.head()
| PC1 | PC2 | |
|---|---|---|
| 0 | 16182.883841 | 11361.067783 |
| 1 | -4061.823251 | 671.046015 |
| 2 | -4139.749681 | 753.702571 |
| 3 | -3581.416594 | 8.070269 |
| 4 | -4538.893994 | 135.636784 |
df_pca['salary'] = np.array(y)
df_pca.head()
| PC1 | PC2 | salary | |
|---|---|---|---|
| 0 | 16182.883841 | 11361.067783 | 1161 |
| 1 | -4061.823251 | 671.046015 | 600 |
| 2 | -4139.749681 | 753.702571 | 379 |
| 3 | -3581.416594 | 8.070269 | 651 |
| 4 | -4538.893994 | 135.636784 | 497 |
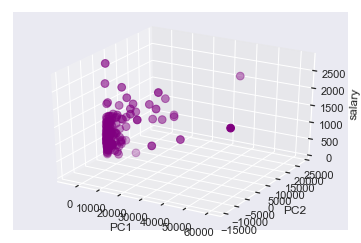
Nyt meidän on mahdollista visualisoida koko datasetti yhteen, kolmiulotteiseen kuvaan. Tästä kuvasta voisimmekin kenties päätellä, että lineaarinen regressiomalli ei välttämättä tule tuottamaan meille kovinkaan hyvää ennustetta palkasta.
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(df_pca['PC1'], df_pca['PC2'], df_pca['salary'], c='purple', s=60)
ax.set_xlabel('PC1')
ax.set_ylabel('PC2')
ax.set_zlabel('salary')
plt.show()
Kohinan filtteröinti PCA:n avulla
PCA on kätevä tekniikka datan tiivistämiseen ja dimension alentamiseen ja korrelaatioiden poistamiseen. Pääkomponenttianalyysia tosin voidaan hyödyntää myös muihin tilanteisiin. Usein dataa hankitaan esimerkiksi sensoreilla mittaamalla. Tällöin datassa saattaa esiintyä kohinaa (noise), joka ei ole osa varsinaista signaalia, vaan häiriöstä johtuvaa satunnaista epätarkkuutta tai mittavirhettä. (Esimerkiksi ääntä nauhoitettaessa taustalta kuuluva kohina.) Katsotaan seuraavaksi miten PCA:ta voidaan hyödyntää mm. kohinan filtteröinnissä datasta.
Kohinan poistaminen PCA:n avulla perustuu siihen, että kaikilla niillä muuttujilla, joilla on selvästi suurempi varianssi kuin kohinan aiheuttama varianssi, kohina ei juurikaan vaikuta muunnoksen lopputulokseen. Ts. rekonstruoimalla datan pelkästään pääkomponenttien avulla, hyvin todennäköisesti pidämme juuri olennaisen signaalin ja hävitämme kohinan. Tutkitaan tällä kertaa klassista käsinpiirrettyjen numeroiden datasettiä ja havainnollistetaan tätä tekniikkaa:
# Aloitetaan taas tuomalla datasetti. Tämä kyseinen data on hyvin yleisesti käytössä erilaisissa tutoriaaleissa,
# ja löytyykin siksi valmiina sklearn-kirjaston dataseteistä.
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
(1797, 64)
Tämä kyseinen data koostuu siis 8×8 pikselisistä kuvista, ts. data on 64-dimensioista. Piirretään vielä muutamia esimerkkikuvia, jotta saadaan hyvä käsitys datasta.
# Käytetään taas matplotlibiä kuvien piirtelemiseen
def plot_digits(data):
# Käytetään subplotteja siten, että saadaan kaikki numerot samaan kuvaan
fig, axes = plt.subplots(4, 10, figsize=(10, 4),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8, 8),
cmap='binary', interpolation='nearest',
clim=(0, 16))
# Kutsutaan funktiota
plot_digits(digits.data)
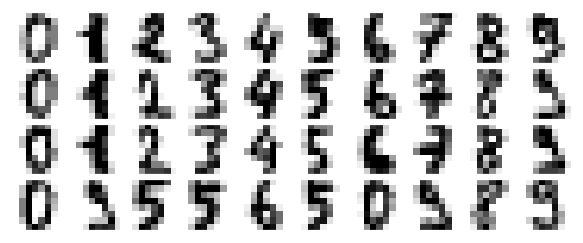
Lisätään seuraavaksi itse hieman kohinaa dataan, ja piirrellään kuvat uudestaan
np.random.seed(42)
noisy = np.random.normal(digits.data, 4)
plot_digits(noisy)
# Sovitetaan nyt PCA tähän uuteen dataan siten, että säilytetään 50% varianssista, eli ei määritellä suoraan
# jäljelle jäävien komponenttien määrää
pca = PCA(0.50).fit(noisy)
pca.n_components_
12
# Jäljelle jäi 12 saraketta alkuperäisestä 64:stä. Tämä muunnos siis säilytti 50% alkuperäisestä varianssista. Otetaan
# seuraavaksi muunnos tämän mallin avulla datasta, ja lopulta rekonstruoidaan data käänteis-muunnoksella.
components = pca.transform(noisy)
filtered = pca.inverse_transform(components)
plot_digits(filtered)
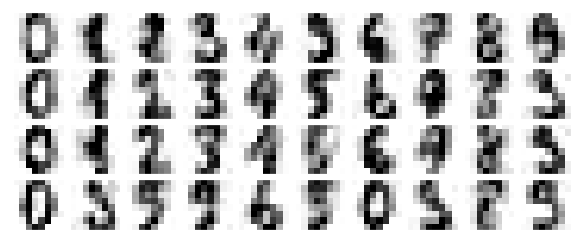
Huomataan, että päästiin melko hyvin eroon kohinasta. Tässä piilee myös yksi PCA:n hienous datan esikäsittelyn kannalta. Sen sijaan, että esimerkiksi koulutettaisiin malli erittäin monidimensioisella datalla, voidaankin kouluttaa malli hieman matalampi-dimensioisella esityksellä samasta datasta, joka myös hoitaa kohinan filtteröinnin ja korrelaatioiden poistamisen yhdellä iskulla. Lisää esimerkkejä PCA:n käytöstä löydät mm. Python Data Science Handbookista.