Lineaarinen regressio
Voit ladata tehtävät tästä. Malliratkaisut löytyvät täältä. Voit myös ladata nämä materiaalit muistiona tästä.
Lineaarinen regressio: materiaali
Tällä kertaa tutustumme lineaariseen regressioon. Lineaarinen regressio on hyvä malli silloin, kun halutaan tutkia joidenkin tekijöiden vaikutusta jatkuvaan muuttujaan: esimerkiksi tänään pohdimme palkkoja ja myyntiä. Se on hyvä yleismalli, jota on syytä kokeilla aina ensin vastaavissa tapauksissa. Sen ennustevoima on monesti aika rajallinen, mutta analysoimalla lineaarista regressiomallia ja visualisoimalla dataa sen tueksi saadaan tärkeää tietoa siitä, mitä tehdä seuraavaksi, jos yksinkertainen malli ei riitä.
Jotta elämä ei kävisi liian tylsäksi, tutustumme myös pariin uuteen data scientistin työkaluun. Lisäämme lineaariseen regressioon sääntelytermin (engl. regulation). Sitten katselemme ristiinvalidointia ja lopuksi vilkaisemme lyhyesti muuttujien standardisoimista. Nämä menetelmät soveltuvat myös logistisen regression tapauksessa ja kiinnostuneille suosittelemmekin vahvasti toistamaan analyysin käyttämällä viime kerran materiaaleja.
Tänään pääset siis jälleen pohtimaan erilaisia data science -tehtäviä. Ensimmäisessä tehtävässä toimit headhunterina, joka välittää yritysjohtajia ja yrittää arvioida näiden palkkaa käyttämällä avukseen data science -menetelmiä. Toisessa tehtävässä olet töissä ison yrityksen markkinointiosastolla ja tehtävänäsi on ennustaa markkinoinnin vaikutusta myyntiin. Edellisen kerran tapaan esimerkeissä käytetyt datasetit ovat aitoja, mutta niiden ympärille rakennetut tarinat keksittyjä.
Käymme jälleen ensin mallia läpi yhdessä ensimmäisen tehtävän avulla. Toinen tehtävä jätetään harjoitustyöksi. Aluksi jutellaan myös hetki teoriasta.
Ensimmäinen tehtävä: yritysjohtajan palkan ennustaminen
Olet siis töissä headhunter-yrityksessä ja tehtävänäsi on etsiä yrityksille johtajia. Saat työstäsi palkkion jokaisen onnistuneen rekrytoinnin johdosta. Saamasi palkkio riippuu johtajan palkasta uudessa työpaikassa. Haaveilet siis nappailevasi mahdollisimman kovapalkkaisia johtajia.
Internetistä lukemasi perusteella arvelet, että voisit käyttää johtajien palkan ennustamiseen koneoppimisen menetelmiä. Pienellä vaivalla saat käsiisi datasetin, josta on kuvaus alla
Obs: 177
- salary 1990 compensation, $1000s
- age in years
- college = 1 if attended college
- grad = 1 if attended graduate school
- comten years with company
- ceoten years as ceo with company
- sales 1990 firm sales, millions
- profits 1990 profits, millions
- mktval market value, end 1990, mills.
- lsalary log(salary)
- lsales log(sales)
- lmktval log(mktval)
- comtensq comten^2
- ceotensq ceoten^2
- profmarg profits as % of sales
Lyhyt katsaus teoriaan
Lineaarinen regressio siis arvio yritysjohtajan palkkaa erilaisten tekijöiden, kuten yrityksen myynnin tai markkina-arvon funktiona. Matemaattisesti kuvattuna \begin{equation} y = \beta_0 + \beta_1 x_1 + … + \beta_n x_n . \tag{1} \end{equation} Yhtälössä (1) $ y $ on selitettävä eli endogeeninen muuttuja, tässä yritysjohtajan palkka. $ x_1, …, x_n $ ovat eksogeenisia eli selittäviä muuttujia ja niiden arvot saadaan datasta. Regressiokertoimet $ \beta_0, …, \beta_n $ estimoidaan mallin avulla.
Lineaarisen regression tapauksessa regressiokertoimilla on selkeä tulkinta. $ \beta_0 $ on vakiotermi, joka kertoo yrityksen johtajan palkan silloin, kun kaikki selittävät tekijät saavat arvon 0. Esimerkiksi tehtäväosuudessa se kuvaa myynnin määrää silloin, kun yritys ei käytä rahaa mainontaan. $ \beta_1, …, \beta_n $ kertovat kunkin selittävän muuttujan vaikutuksen palkkaan, esimerkiksi kuinka paljon enemmän tai vähemmän palkkaa vanhempi yritysjohtaja saa nuorempaan verrattuna.
Regression selitysvoimaa voi usein parantaa lisäämällä erilaisia muunnoksia selittävistä tekijöistä, kuten logaritmeja tai polynomeja. Käytämme luento-osuudessa muuttujista myös seuraavanlaisia muotoja \begin{equation} \log y = \beta_0 + \beta_1 \log x_1 + \beta_2 x_2^2 + … + \beta_n x_n . \tag{2} \end{equation} Kutsutaan muuttujaa tasomuuttujaksi, jos se on on muotoa $ x_i $ ja log-muuttujaksi, jos se on muotoa $ \log x_i $. Logaritmisilla termeillä kuvataan prosenttimuutoksia.
Logaritmisten ja tasomuuttujien kertoimilla voidaan esittää selkeä tulkinta, jota voidaan havainnollistaa seuraavan taulukon avulla
| Malli | Engoneeninen muuttuja | Eksogeeninen muuttuja | Kertoimen $ \beta_1 $ tulkinta |
|---|---|---|---|
| taso - taso | $ y $ | $ x $ | $ \Delta y = \beta_1 \Delta x $ |
| taso - log | $ y $ | $ \log x $ | $ \Delta y = (\beta_1/100)\% \Delta x $ |
| log - taso | $ \log y $ | $ x $ | $ \% \Delta y = (100\beta_1) \Delta x $ |
| log - log | $ \log y $ | $ \log x $ | $ \% \Delta y = \beta_1\% \Delta x $ |
Lisäksi käsittelemme regression sääntelyä. Rajoitamme tarkastelun kahteen tapaukseen: lassoon (engl. least absolute shrinkage and selection operator) ja harjanneregressioon (engl. ridge). Tarkastelemme ääritapauksia havainnollisuuden vuoksi; käytännössä usein käytetään yhdistelmiä ja muitankin menetelmiä on. Sääntelyn tarkoituksena on suojella mallia ylisovittamiselta ja sääntelymallit rankaisevat mallia monimutkaisuudesta. Tarkemmin lasso rankaisee mallia muuttujien määrästä ja harjanne koosta. Lasso siis yksinkertaistaa mallia vähentämällä selittävien tekijöiden määrää ja harjanne yrittää estää vaikkapa tilannetta, jossa yksi muuttuja dominoisi analyysia.
Data
Aloitamme jälleen tehtävän datantarkastelulla. Käytetään Pandas-kirjastoa ja tulostetaan muistikirjaan datasetin ensimmäiset rivit ja muoto.
import pandas as pd
# data avattu suomenkielisessä excelissä, joten desimaalit on eroteltu pilkulla ja solut puolipisteellä
# jos datasettisi on samassa kansiossa, poista alta '../data/'
df = pd.read_csv('../data/ceosal2.csv', sep = ';', decimal = ',')
df.tail()
| salary | age | college | grad | comten | ceoten | sales | profits | mktval | lsalary | lsales | lmktval | comtensq | ceotensq | profmarg | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 172 | 264 | 63 | 1 | 0 | 42 | 3 | 334 | 43 | 480 | 5.575949 | 5.811141 | 6.173786 | 1764 | 9 | 12.874250 |
| 173 | 185 | 58 | 1 | 0 | 39 | 1 | 766 | 49 | 560 | 5.220356 | 6.641182 | 6.327937 | 1521 | 1 | 6.396867 |
| 174 | 387 | 71 | 1 | 1 | 32 | 13 | 432 | 28 | 477 | 5.958425 | 6.068426 | 6.167517 | 1024 | 169 | 6.481482 |
| 175 | 2220 | 63 | 1 | 1 | 18 | 18 | 277 | -80 | 540 | 7.705263 | 5.624018 | 6.291569 | 324 | 324 | -28.880870 |
| 176 | 445 | 69 | 1 | 0 | 23 | 0 | 249 | 31 | 828 | 6.098074 | 5.517453 | 6.719013 | 529 | 0 | 12.449800 |
df.shape
(177, 15)
Muistat lukeneesi, että analyysi kannattaa aina aloittaa piirtämällä muuttujista kuvia. Googlen avulla löydät nk. laatikko ja viikset -kuvion (engl. boxplot/ box-and-whisker plot), joka näyttäisi visualisoivan hyvin jatkuvan muuttujan jakaumaa. Päätät piirtää sellaisen
import seaborn as sns
import matplotlib.pyplot as plt
sns.set()
sns.boxplot(data = df, y = 'salary')
<matplotlib.axes._subplots.AxesSubplot at 0x1a1f35f470>
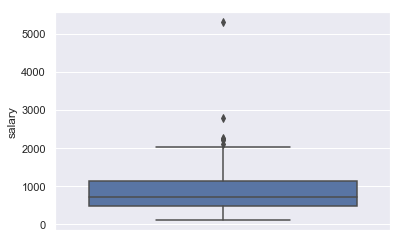
Huomaat, että aineistossasi on johtaja, jolla on muihin nähden poikkeuksellisen korkea palkka. Päätät jäädä tutkistelemaan tilannetta.
Kokeneena rekrytoijana huomiosi kiinnittyy myös muuttujaan ‘college’, joka tuntuu saavan arvon 1 jokaiselle datasetissä esiintyvälle johtajalle. Näppituntumasi sanoo, että suurin osa kohtaamistasi yritysjohtajista on suorittanut collegen. Muistelet kuulleesi, että regressiossa ei ole hyvä olla muuttujia, joista on vain hyvin vähän havaintoja jossakin kategoriassa. Päätät ottaa kyseisestä muuttujasta tarkemmin selvää. Aloitat piirtämällä kuvan.
sns.countplot(x = 'college', data = df)
plt.show()
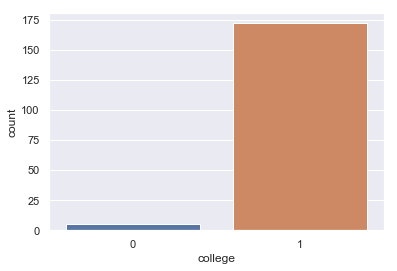
Huomaat, että aineistossasi on todella vähän johtajia, jotka eivät ole käyneet collegea. Varmuuden vuoksi päätät tulostaa taulukon, joka kertoo, kuinka monta.
taulukko = pd.crosstab(index = df['college'], columns = 'count')
# nimetään taulukon osat niin, että lopputulos on hyvin ymmärrettävissä
taulukko.columns = ['lukumäärä']
taulukko.index = ['ei collegea', 'college']
# tulostetaan vielä valmis taulukko
taulukko
| lukumäärä | |
|---|---|
| ei collegea | 5 |
| college | 172 |
Muistelet joskus kuulleesi nyrkkisäännön, jonka mukaan muuttujaa ei saa ottaa mukaan analyysiin, jos sillä ei ole vähintään viittä arvoa kategoriassa. Olet hieman epäileväinen ja päätät toistaa aiemman laatikkokuvasi, mutta tällä kertaa piirtää erillisen laatikon collegen suorittamisen mukaan.
sns.boxplot(data = df, x = 'college', y = 'salary')
plt.show()
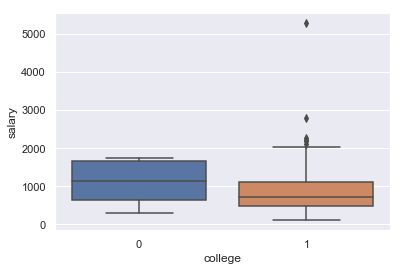
Huomaat, että jakauma on melko epätasainen; collegen käymättömillä on huomattavasti suurempi palkka. Pelkäät, että tämä muuttuja vääristää analyysiasi, joten päätät poistaa muuttujan aineistostasi.
df = df.drop(['college'], axis = 1)
Seuraavaksi huomaat, että aineistossasi on sekä taso- että log-muuttujia. Tulostat tiedot muuttujista muistisi virkistämiseksi.
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 177 entries, 0 to 176
Data columns (total 14 columns):
salary 177 non-null int64
age 177 non-null int64
grad 177 non-null int64
comten 177 non-null int64
ceoten 177 non-null int64
sales 177 non-null int64
profits 177 non-null int64
mktval 177 non-null int64
lsalary 177 non-null float64
lsales 177 non-null float64
lmktval 177 non-null float64
comtensq 177 non-null int64
ceotensq 177 non-null int64
profmarg 177 non-null float64
dtypes: float64(4), int64(10)
memory usage: 19.4 KB
Päätät jakaa aineistosi kahteen osaan: toiseen keräät tasomuuttujia ja toiseen log-muuttujia. Analyysisi aiot suorittaa varmuuden vuoksi molemmilla.
df_taso = df.drop(['lsalary', 'lsales', 'lmktval'], axis = 1)
df_log = df.drop(['salary', 'sales', 'mktval'], axis = 1)
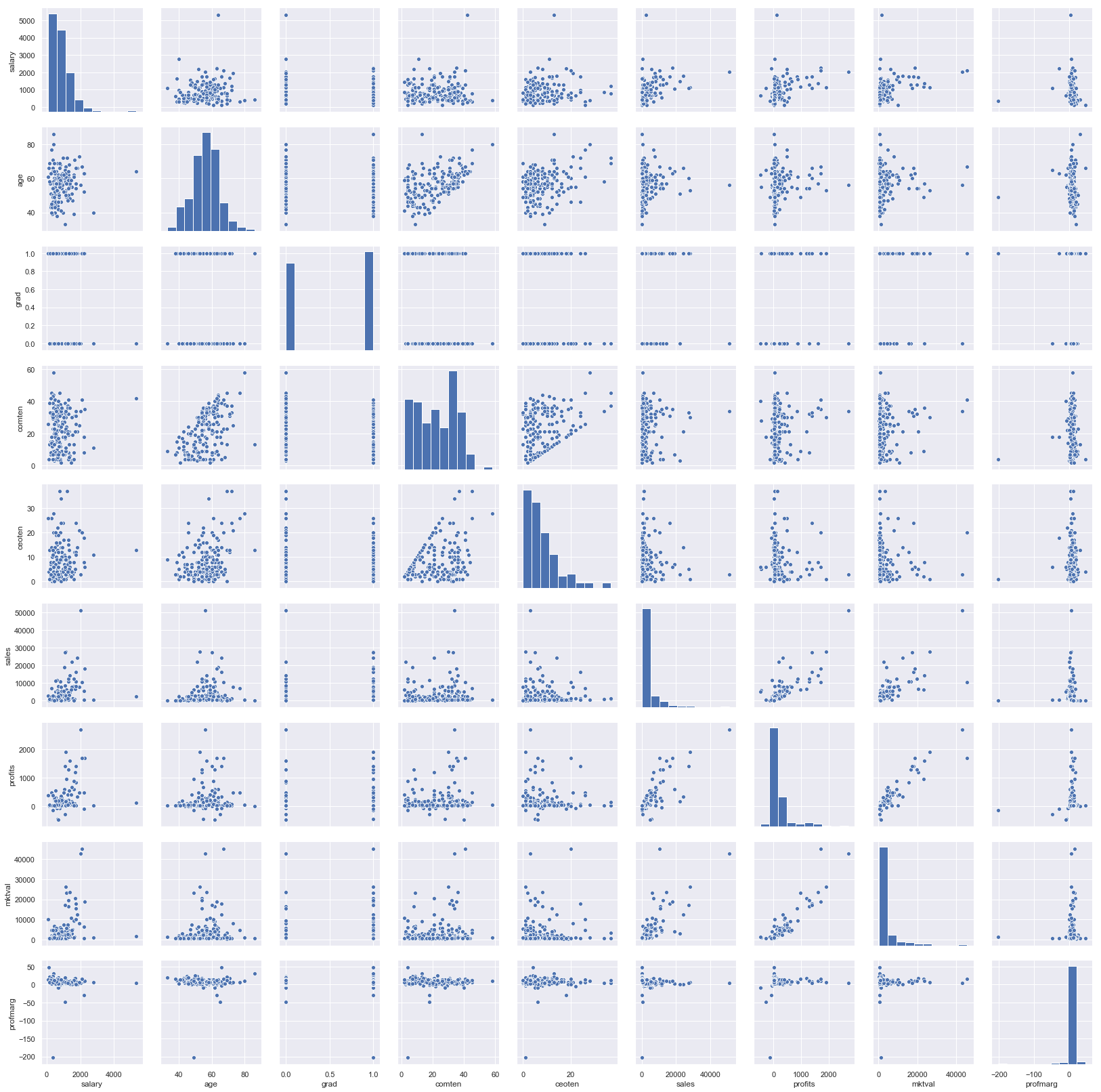
Aineistossasi on melko melko monta muuttujaa ja haluat saada niistä tarkemman kuvat. Havainnollistamiseksi aloitat piirtämällä parittaiset kuvat.
# jätetään neliömuotoiset muuttujat pois
sns.pairplot(df_taso.drop(['comtensq', 'ceotensq'], axis = 1))
plt.show()
sns.pairplot(df_log.drop(['comtensq', 'ceotensq'], axis = 1))
plt.show()
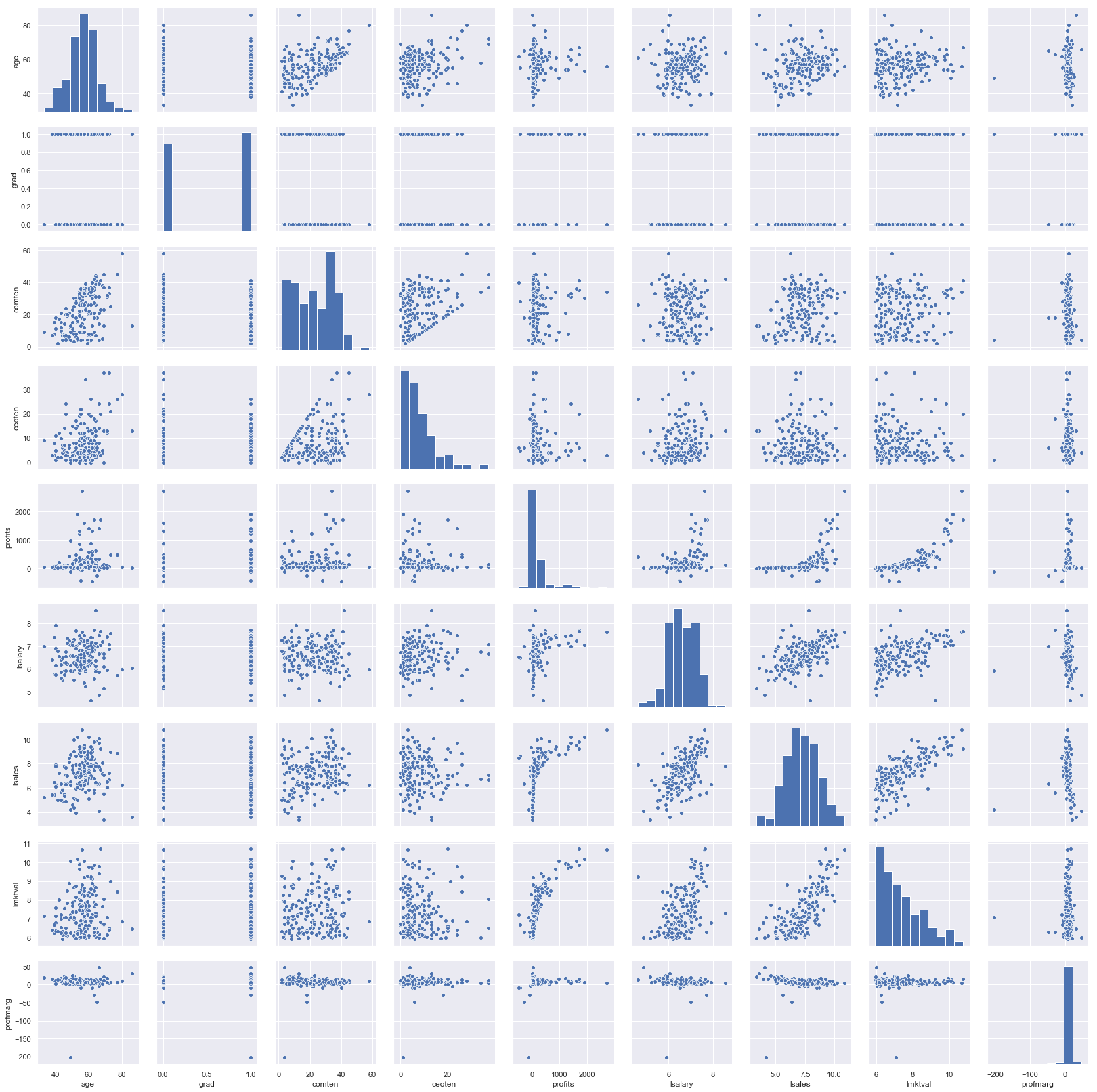
Hieman huolestuneena tarkastelet havaintoasi, jolla on poikkeuksellisen korkea palkka. Kyseinen johtaja tuntuu olevan vanhempaa ikäpolvea ja toiminut pitkään yrityksessä. Yrityksen tulos ja markkina-arvo eivät kuitenkaan vaikuta kovinkaan lupaavilta. Arvelet, että kyseinen havainto ei ole näkökulmastasi katsoen kovinkaan relevantti ja pelkäät sen vääristävän analyysiasi. Poistat sen siis aineistostasi.
df_taso = df_taso[df_taso.salary < 5000]
df_log = df_log[df_log.lsalary < 8.2]
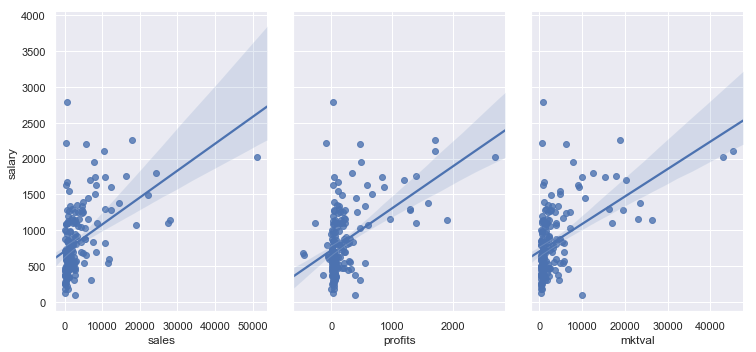
Valitset vielä pari muuttujaa, jotka arvioit tärkeiksi ja piirrät niistä erillisen kuvan. Lisäät kuviin regressiosuoran tilanteen havainnollistamiseksi.
sns.pairplot(df_taso, x_vars = ['sales', 'profits', 'mktval'], y_vars = 'salary',
height = 5, aspect = 0.7,
kind = 'reg')
plt.show()
/anaconda3/lib/python3.6/site-packages/scipy/stats/stats.py:1713: FutureWarning: Using a non-tuple sequence for multidimensional indexing is deprecated; use `arr[tuple(seq)]` instead of `arr[seq]`. In the future this will be interpreted as an array index, `arr[np.array(seq)]`, which will result either in an error or a different result.
return np.add.reduce(sorted[indexer] * weights, axis=axis) / sumval
sns.pairplot(df_log, x_vars = ['lsales', 'profits', 'lmktval'], y_vars = 'lsalary',
height = 5, aspect = 0.7,
kind = 'reg')
plt.show()
/anaconda3/lib/python3.6/site-packages/scipy/stats/stats.py:1713: FutureWarning: Using a non-tuple sequence for multidimensional indexing is deprecated; use `arr[tuple(seq)]` instead of `arr[seq]`. In the future this will be interpreted as an array index, `arr[np.array(seq)]`, which will result either in an error or a different result.
return np.add.reduce(sorted[indexer] * weights, axis=axis) / sumval
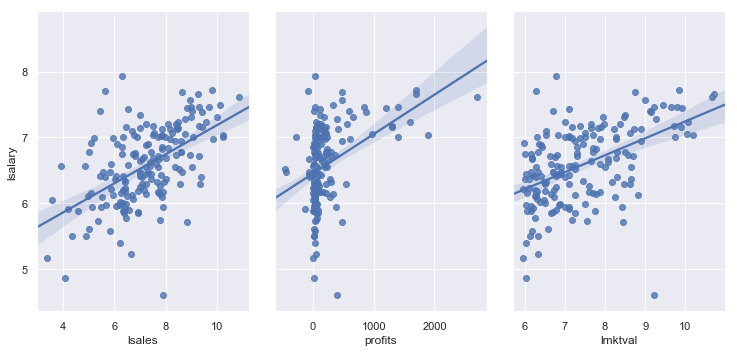
Muistelet myös lukeneesi varoituksia multikollineariteetista ja siitä, että se saattaa vaikuttaa analyysisi luotettavuuteen. Päätät tarkastaa muuttujien väliset korrelaatiot.
corr = df_taso.drop(['comtensq', 'ceotensq'], axis = 1).corr()
corr
| salary | age | grad | comten | ceoten | sales | profits | mktval | profmarg | |
|---|---|---|---|---|---|---|---|---|---|
| salary | 1.000000 | 0.093506 | 0.052210 | -0.037605 | 0.137190 | 0.472663 | 0.491158 | 0.511900 | -0.030931 |
| age | 0.093506 | 1.000000 | -0.118367 | 0.475791 | 0.336373 | 0.128396 | 0.116156 | 0.109139 | 0.015134 |
| grad | 0.052210 | -0.118367 | 1.000000 | -0.221019 | -0.098988 | 0.075452 | 0.096819 | 0.121427 | -0.015943 |
| comten | -0.037605 | 0.475791 | -0.221019 | 1.000000 | 0.311414 | 0.106862 | 0.146806 | 0.140103 | 0.048264 |
| ceoten | 0.137190 | 0.336373 | -0.098988 | 0.311414 | 1.000000 | -0.067069 | -0.020754 | 0.007937 | 0.049206 |
| sales | 0.472663 | 0.128396 | 0.075452 | 0.106862 | -0.067069 | 1.000000 | 0.798243 | 0.754619 | -0.017442 |
| profits | 0.491158 | 0.116156 | 0.096819 | 0.146806 | -0.020754 | 0.798243 | 1.000000 | 0.918124 | 0.125396 |
| mktval | 0.511900 | 0.109139 | 0.121427 | 0.140103 | 0.007937 | 0.754619 | 0.918124 | 1.000000 | 0.066888 |
| profmarg | -0.030931 | 0.015134 | -0.015943 | 0.048264 | 0.049206 | -0.017442 | 0.125396 | 0.066888 | 1.000000 |
Ylläoleva taulukko vaikuttaa hieman sekavalta, joten havainnollistat asiaa kuvan avulla.
sns.heatmap(corr)
plt.xticks(range(len(corr.columns)), corr.columns)
plt.yticks(range(len(corr.columns)), corr.columns)
plt.show()
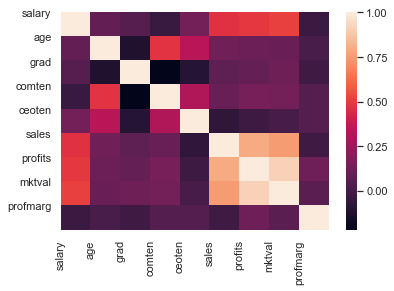
Huomaat, että yrityksen voiton ja markkina-arvon välillä on todella iso korrelaatio. Pidät tämän mielessäsi ja toistat saman logaritmisille muuttujille.
corr = df_log.drop(['comtensq', 'ceotensq'], axis = 1).corr()
corr
| age | grad | comten | ceoten | profits | lsalary | lsales | lmktval | profmarg | |
|---|---|---|---|---|---|---|---|---|---|
| age | 1.000000 | -0.118367 | 0.475791 | 0.336373 | 0.116156 | 0.076234 | 0.192454 | 0.131729 | 0.015134 |
| grad | -0.118367 | 1.000000 | -0.221019 | -0.098988 | 0.096819 | 0.034253 | 0.086143 | 0.150145 | -0.015943 |
| comten | 0.475791 | -0.221019 | 1.000000 | 0.311414 | 0.146806 | -0.033385 | 0.236128 | 0.103368 | 0.048264 |
| ceoten | 0.336373 | -0.098988 | 0.311414 | 1.000000 | -0.020754 | 0.104910 | -0.039313 | -0.043225 | 0.049206 |
| profits | 0.116156 | 0.096819 | 0.146806 | -0.020754 | 1.000000 | 0.413859 | 0.607158 | 0.776922 | 0.125396 |
| lsalary | 0.076234 | 0.034253 | -0.033385 | 0.104910 | 0.413859 | 1.000000 | 0.539875 | 0.498568 | -0.059606 |
| lsales | 0.192454 | 0.086143 | 0.236128 | -0.039313 | 0.607158 | 0.539875 | 1.000000 | 0.736416 | -0.014420 |
| lmktval | 0.131729 | 0.150145 | 0.103368 | -0.043225 | 0.776922 | 0.498568 | 0.736416 | 1.000000 | 0.060745 |
| profmarg | 0.015134 | -0.015943 | 0.048264 | 0.049206 | 0.125396 | -0.059606 | -0.014420 | 0.060745 | 1.000000 |
sns.heatmap(corr)
plt.xticks(range(len(corr.columns)), corr.columns)
plt.yticks(range(len(corr.columns)), corr.columns)
plt.show()
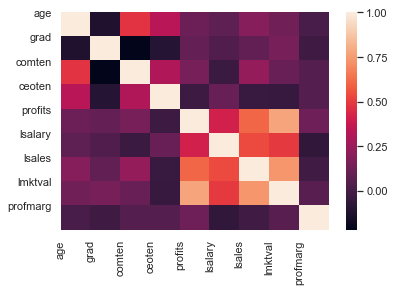
Yllätykseksesi huomaat, että tilanne on huomattavasti parempi. Päätät jatkaa analyysia ja olla tekemättä muutoksia dataan.
Harjoitusdata ja testidata
Seuraava askeleesi on jakaa datasettisi harjoitus- ja testidataan. (Jos kaipaat muistinvirkistämistä, tästä on lisää viime kerran materiaaleissa.)
X = df_taso.drop(['salary'], axis = 1)
y = df_taso.salary
logX = df_log.drop(['lsalary'], axis = 1)
logy = df_log.lsalary
X.head()
| age | grad | comten | ceoten | sales | profits | mktval | comtensq | ceotensq | profmarg | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 49 | 1 | 9 | 2 | 6200 | 966 | 23200 | 81 | 4 | 15.580650 |
| 1 | 43 | 1 | 10 | 10 | 283 | 48 | 1100 | 100 | 100 | 16.961130 |
| 2 | 51 | 1 | 9 | 3 | 169 | 40 | 1100 | 81 | 9 | 23.668640 |
| 3 | 55 | 0 | 22 | 22 | 1100 | -54 | 1000 | 484 | 484 | -4.909091 |
| 4 | 44 | 1 | 8 | 6 | 351 | 28 | 387 | 64 | 36 | 7.977208 |
type(X)
pandas.core.frame.DataFrame
X.shape
(176, 10)
y.head()
0 1161
1 600
2 379
3 651
4 497
Name: salary, dtype: int64
type(y)
pandas.core.series.Series
y.shape
(176,)
Käytetään tällä kertaa sklearn.model_selection-moduulin valmista funktiota datan jakamiseen.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 42)
logX_train, logX_test, logy_train, logy_test = train_test_split(logX, logy, random_state = 42)
X_train.shape
(132, 10)
X_test.shape
(44, 10)
Lineaarinen regressio
Valitset mallin sovittamiseen sklearn.linear_model-moduulin lineaarisen regression funktion. Luot oman funktion taso- ja log-malleille.
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
llinreg = LinearRegression()
# sovitetaan regressio harjoitusdataan
linreg.fit(X_train, y_train)
llinreg.fit(logX_train, logy_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
Seuraavaksi tarkastelet tarkemmin mallin kertoimia saadaksesi käsityksen siitä, miten johtajan palkka määräytyy mallissasi.
# tulostetaan regressiovakion arvo
linreg.intercept_
220.2136987996373
llinreg.intercept_
4.183109984544585
# kerätään muuttujien nimet vektoreihin ja tehdään näistä lista
coef_names = ['age', 'grad', 'comten', 'ceoten', 'sales', 'profits',
'mktval', 'comtensq', 'ceotensq', 'profmarg']
l_coef_names = ['age', 'grad', 'comten', 'ceoten', 'lsales', 'profits',
'lmktval', 'comtensq', 'ceotensq', 'profmarg']
coefs = zip(coef_names, linreg.coef_)
lcoefs = zip(l_coef_names, llinreg.coef_)
coefs = list(coefs)
print(coefs)
print("")
lcoefs = list(lcoefs)
print(lcoefs)
[('age', 6.399752836474609), ('grad', -48.250285264265514), ('comten', 5.963189854211676), ('ceoten', 47.01512366190105), ('sales', 0.0075631522630478475), ('profits', 0.2014484652167957), ('mktval', 0.022479460466437336), ('comtensq', -0.340481855141601), ('ceotensq', -1.1743817788953776), ('profmarg', -1.7719171160206877)]
[('age', 0.0023935003369461886), ('grad', -0.07740034159291824), ('comten', 0.001011968332119664), ('ceoten', 0.04655759585997374), ('lsales', 4.738812609085091e-05), ('profits', 0.14849523834181788), ('lmktval', 0.1539703370607295), ('comtensq', -0.0002750235953702351), ('ceotensq', -0.0009124357641041714), ('profmarg', -0.002190139605817343)]
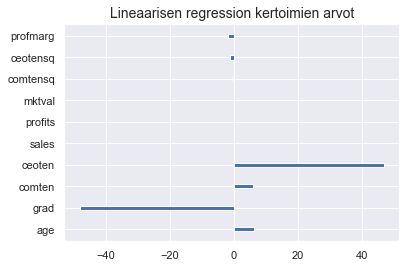
Tilanteen havainnollistamiseksi kuvan piirtäminen on jälleen hyvä idea.
plt.barh(y = X.columns, width = linreg.coef_, height = 0.2)
plt.title("Lineaarisen regression kertoimien arvot", fontsize = 14)
plt.show()
plt.barh(y = logX.columns, width = llinreg.coef_, height = 0.2)
plt.title("Lineaarisen regression kertoimien arvot logaritmiselle mallille", fontsize = 14)
plt.show()
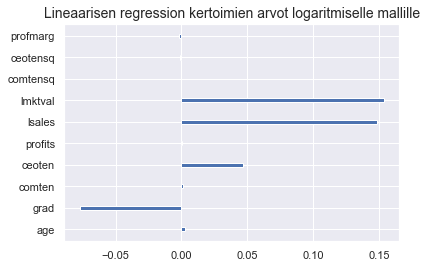
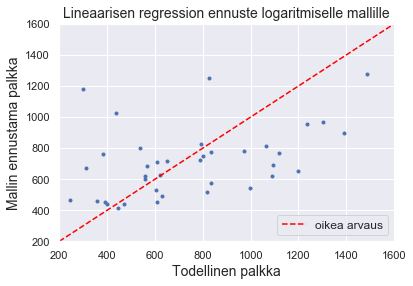
Hieman ihmettelet muuttujan grad negatiivista arvoa, mutta muistat, että myös collegen käyneiden yritysjohtajien palkka oli pienempi kun käymättömien. Alat epäillä, että kouluttautuneiden on helpompi päästä yritysjohtajiksi. Myynnin ja yrityksen markkina-arvon vaikutus näyttää kadonneen tasomallista, kun taas log-mallissa on havaittavissa selkeä vaikutus. Epäilet, että tämä johtuu muuttujien välisestä multikollineariteetista.
Kokeilet mallilla ennustamista parilla esimerkillä. Logaritmisen mallin palkasta on otettava eksponentiaali jotta saadaan palkan taso.
linreg.predict(X_test[0:3])
array([441.53704015, 547.14013921, 574.09782961])
X_test[0:3]
| age | grad | comten | ceoten | sales | profits | mktval | comtensq | ceotensq | profmarg | |
|---|---|---|---|---|---|---|---|---|---|---|
| 19 | 58 | 0 | 36 | 1 | 1100 | 69 | 880 | 1296 | 1 | 6.272727 |
| 45 | 64 | 0 | 44 | 8 | 571 | 57 | 670 | 1936 | 64 | 9.982487 |
| 140 | 40 | 0 | 18 | 1 | 2400 | 60 | 1300 | 324 | 1 | 2.500000 |
y_test[0:3]
19 609
45 401
140 310
Name: salary, dtype: int64
import numpy as np
np.exp(llinreg.predict(logX_test[0:3]))
array([455.29197106, 440.43486507, 672.31593934])
Olet hieman huolissasi mallisi suorituskyvystä ja päätät laskea mallin selitysasteen ($ R^2 $) testidatasi avulla eli tarkastaa, kuinka monta prosenttia mallisi selittää yritysjohtajan palkasta.
linreg.score(X_test, y_test)
0.1665283727242004
llinreg.score(logX_test, logy_test)
0.10607108847310853
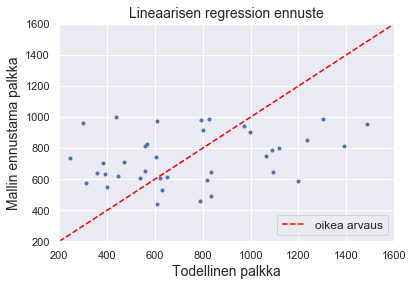
Et ole kovin tyytyväinen tulokseen, mutta ennustat vielä mallisi avulla testidatasi ja havainnollistat mallin tuloksia kuvien avulla.
pred = linreg.predict(X_test)
lpred = llinreg.predict(logX_test)
plt.plot(y_test, pred, '.')
plt.plot([200, 1600], [200, 1600], linestyle='--', color = 'red', label = "oikea arvaus")
plt.xlim([200, 1600]), plt.ylim([200, 1600])
plt.title("Lineaarisen regression ennuste", fontsize = 14)
plt.xlabel('Todellinen palkka', fontsize = 14)
plt.ylabel('Mallin ennustama palkka', fontsize = 14)
plt.legend(loc = 4, fontsize = 12)
plt.show()
plt.plot(y_test, np.exp(lpred), '.')
plt.plot([200, 1600], [200, 1600], linestyle='--', color = 'red', label = "oikea arvaus")
plt.xlim([200, 1600]), plt.ylim([200, 1600])
plt.title("Lineaarisen regression ennuste logaritmiselle mallille", fontsize = 14)
plt.xlabel('Todellinen palkka', fontsize = 14)
plt.ylabel('Mallin ennustama palkka', fontsize = 14)
plt.legend(loc = 4, fontsize = 12)
plt.show()
Säännelty regressio
Olet nyt erittäin huolissasi mallistasi, mutta päätät vielä kokeilla, auttaisiko mallin säännöstely asiaa. Aloitat lassolla.
from sklearn.linear_model import Lasso
lasso = Lasso()
llasso = Lasso()
lasso.fit(X_train, y_train)
llasso.fit(logX_train, logy_train)
Lasso(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=1000,
normalize=False, positive=False, precompute=False, random_state=None,
selection='cyclic', tol=0.0001, warm_start=False)
Jälleen tarkastat mallin kertoimet.
lasso.intercept_
218.80039574105297
llasso.intercept_
6.509699511486989
coefs = zip(coef_names, lasso.coef_)
lcoefs = zip(coef_names, llasso.coef_)
coefs = list(coefs)
lcoefs = list(lcoefs)
print(coefs)
print("")
print(lcoefs)
[('age', 6.390229703497373), ('grad', -43.90801086688294), ('comten', 5.897803548209496), ('ceoten', 46.882976677209726), ('sales', 0.007595655454173405), ('profits', 0.20102540288953658), ('mktval', 0.022444026622450302), ('comtensq', -0.338287507139723), ('ceotensq', -1.1684953767623079), ('profmarg', -1.7656584523098515)]
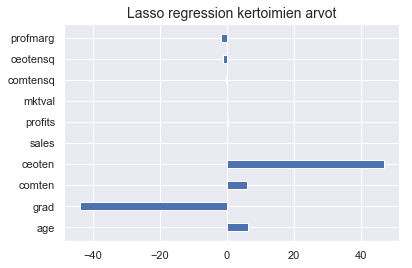
[('age', 0.0), ('grad', -0.0), ('comten', 0.0), ('ceoten', 0.0), ('sales', 0.0006302714323634822), ('profits', 0.0), ('mktval', 0.0), ('comtensq', -0.00018538564891745426), ('ceotensq', 0.0006304797687097125), ('profmarg', -2.7757959198412285e-06)]
Huomaat, että useiden muuttujien arvot ovat kadonneet kokonaan ja muistat, että lasso nimenomaan yksinkertaistaa mallia rankaisemalla liian monen selittävän tekijän käytöstä. Piirrät vielä asiaa havainnollistavan kuvan.
plt.barh(y = X.columns, width = lasso.coef_, height = 0.4)
plt.title("Lasso regression kertoimien arvot", fontsize = 14)
plt.show()
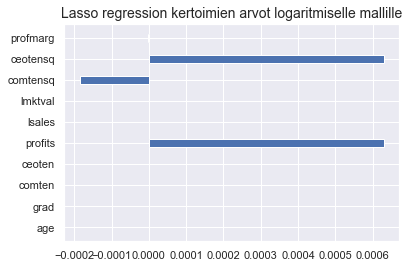
plt.barh(y = logX.columns, width = llasso.coef_, height = 0.4)
plt.title("Lasso regression kertoimien arvot logaritmiselle mallille", fontsize = 14)
plt.show()
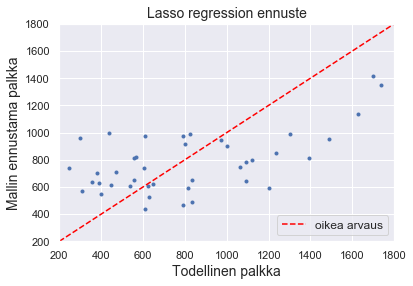
Katsotaan vielä mallin selitysaste ja piirretään kuva mallin ennustamista ja todellisista palkoista.
pred = lasso.predict(X_test)
lpred = llasso.predict(logX_test)
lasso.score(X_test, y_test)
0.16733883201864452
llasso.score(logX_test, logy_test)
-0.029804589118289645
plt.plot(y_test, pred, '.')
plt.plot([200, 1800], [200, 1800], linestyle='--', color = 'red', label = "oikea arvaus")
plt.xlim([200, 1800]), plt.ylim([200, 1800])
plt.title("Lasso regression ennuste", fontsize = 14)
plt.xlabel('Todellinen palkka', fontsize = 14)
plt.ylabel('Mallin ennustama palkka', fontsize = 14)
plt.legend(loc = 4, fontsize = 12)
plt.show()
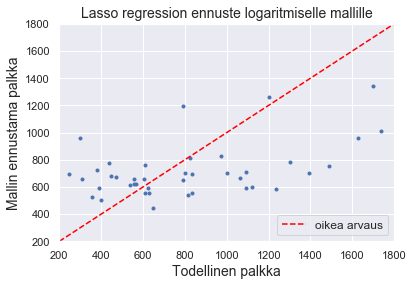
plt.plot(y_test, np.exp(lpred), '.')
plt.plot([200, 1800], [200, 1800], linestyle='--', color = 'red', label = "oikea arvaus")
plt.xlim([200, 1800]), plt.ylim([200, 1800])
plt.title("Lasso regression ennuste logaritmiselle mallille", fontsize = 14)
plt.xlabel('Todellinen palkka', fontsize = 14)
plt.ylabel('Mallin ennustama palkka', fontsize = 14)
plt.legend(loc = 4, fontsize = 12)
plt.show()
Olosi alkaa olla jo vähemmän rohkaistunut, muttä päätät vielä antaa harjanneregressiolle mahdollisuuden.
from sklearn.linear_model import Ridge
ridge = Ridge()
lridge = Ridge()
ridge.fit(X_train, y_train)
lridge.fit(logX_train, logy_train)
Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver='auto', tol=0.001)
ridge.intercept_
219.10338928722388
lridge.intercept_
4.196264871802
coefs = zip(coef_names, ridge.coef_)
lcoefs = zip(coef_names, lridge.coef_)
coefs = list(coefs)
lcoefs = list(lcoefs)
print(coefs)
print("")
print(lcoefs)
[('age', 6.403638235367416), ('grad', -46.710008966603624), ('comten', 5.972193235195459), ('ceoten', 46.95891970660021), ('sales', 0.007568796574042356), ('profits', 0.20134061522651486), ('mktval', 0.022468088436140076), ('comtensq', -0.34042039169897104), ('ceotensq', -1.1719976519940782), ('profmarg', -1.7708730752643915)]
[('age', 0.002440463603831835), ('grad', -0.07488148057408964), ('comten', 0.001084932392639019), ('ceoten', 0.04655086761818114), ('sales', 5.2250462751675984e-05), ('profits', 0.14819745490073713), ('mktval', 0.15171500699209453), ('comtensq', -0.00027641594462789003), ('ceotensq', -0.0009130799162097824), ('profmarg', -0.0021948883327415586)]
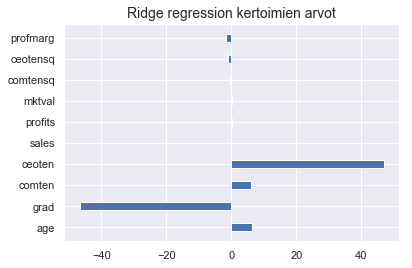
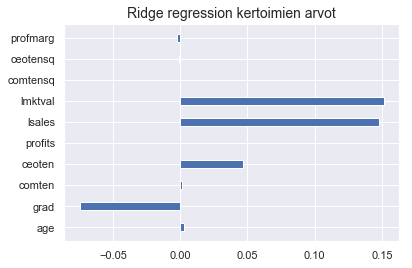
Huomaat, että toisin kuin lasson tapauksessa, selittävien tekijöiden vaikutus tulee taas näkyviin, myös logaritmisessa mallissa.
plt.barh(y = X.columns, width = ridge.coef_, height = 0.4)
plt.title("Ridge regression kertoimien arvot", fontsize = 14)
plt.show()
plt.barh(y = logX.columns, width = lridge.coef_, height = 0.4)
plt.title("Ridge regression kertoimien arvot", fontsize = 14)
plt.show()
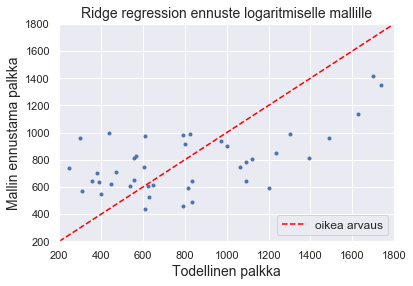
Tuloksesi muistuttavat taas hieman lähemmin lineaarisen regression tuloksia. Hieman jännittyneenä tulostat mallin selitysasteet.
ridge.score(X_test, y_test)
0.16678403503619044
lridge.score(logX_test, logy_test)
0.1068960647955789
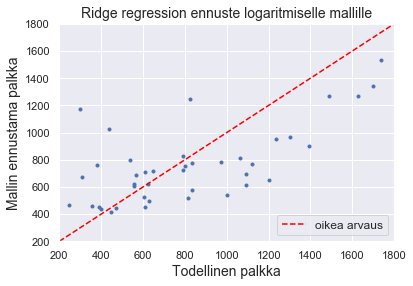
Harjanneregressio tuntuu pärjäävän ainakin lassoa paremmin. Sekin selittää kuitenkin parhaimmillaankin vain noin 17 % treenijoukossa olevien yritysjohtajien palkasta. Piirrät vielä kuvan.
pred = ridge.predict(X_test)
lpred = lridge.predict(logX_test)
plt.plot(y_test, pred, '.')
plt.plot([200, 1800], [200, 1800], linestyle='--', color = 'red', label = "oikea arvaus")
plt.xlim([200, 1800]), plt.ylim([200, 1800])
plt.title("Ridge regression ennuste logaritmiselle mallille", fontsize = 14)
plt.xlabel('Todellinen palkka', fontsize = 14)
plt.ylabel('Mallin ennustama palkka', fontsize = 14)
plt.legend(loc = 4, fontsize = 12)
plt.show()
plt.plot(y_test, np.exp(lpred), '.')
plt.plot([200, 1800], [200, 1800], linestyle='--', color = 'red', label = "oikea arvaus")
plt.xlim([200, 1800]), plt.ylim([200, 1800])
plt.title("Ridge regression ennuste logaritmiselle mallille", fontsize = 14)
plt.xlabel('Todellinen palkka', fontsize = 14)
plt.ylabel('Mallin ennustama palkka', fontsize = 14)
plt.legend(loc = 4, fontsize = 12)
plt.show()
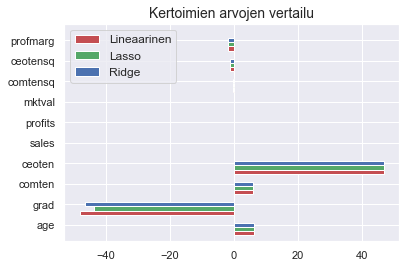
Et ole kovinkaan toiveikas mallisi ennustevoiman suhteen. Haluat kuitenkin ottaa matkasi oppimiskokemuksena ja haluat ymmärtää paremmin regression sääntelyn vaikutusta. Piirrät mallien kertoimet samaan kuvaan horisontaaliseen pylväsdiagrammiin.
# luodaan oma indeksi mallin jokaiselle kertoimelle
ind = np.arange(len(X.columns))
# käytetään matplotlib-kirjaston subplot-funktiota
fig, ax = plt.subplots()
# tehdään jokaisen mallin kertoimille oma pylväs ja väritetään nämä omilla väreillään
ax.barh(y = ind - 0.2, width = linreg.coef_, height = 0.2,
label = "Lineaarinen", color = 'r')
ax.barh(y = ind, width = lasso.coef_, height = 0.2,
label = "Lasso", color = 'g')
ax.barh(y = ind + 0.2, width = ridge.coef_, height = 0.2,
label = "Ridge", color = 'b')
# tulostetaan mallien nimet ja vaihdetaan indeksien tilalle muuttujien nimet
ax.legend(loc = 2, fontsize = 12)
ax.set(yticks = ind + 0.2, yticklabels = coef_names, ylim = [0.4 - 1, len(X.columns)])
ax.set_title("Kertoimien arvojen vertailu", fontsize = 14)
plt.show()
fig, ax = plt.subplots()
ax.barh(y = ind - 0.2, width = llinreg.coef_, height = 0.2,
label = "Lineaarinen", color = 'r')
ax.barh(y = ind, width = llasso.coef_, height = 0.2,
label = "Lasso", color = 'g')
ax.barh(y = ind + 0.2, width = lridge.coef_, height = 0.2,
label = "Ridge", color = 'b')
ax.legend(loc = 2, fontsize = 12)
ax.set_title("Kertoimien arvojen vertailu", fontsize = 14)
ax.set(yticks = ind + 0.2, yticklabels = coef_names, ylim = [0.4 - 1, len(logX.columns)])
plt.show()
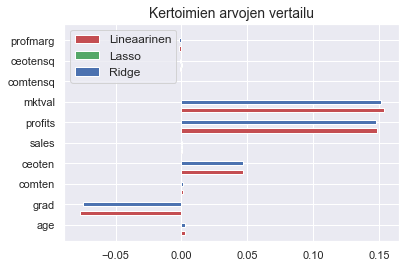
Huomaat, että sääntely hieman häivyttää grad-muuttujan arvoa ja siten yksinkertaistaa hieman malleja. Logistisessa mallissa lasso tuntuu häivyttäneen kertoimien arvon kokonaan, mikä tuntuu mielestäsi melkoiselta ylisäätelyltä.
Ristiinvalidointi ja mallien vertailu
Haluat vielä saada euromääräisen arvion taso-mallisi mittavirheelle. Tätä varten lasket mallillesi neliösummaisen mittavirheen (engl. mean squared error). Kun tästä tunnusluvusta ottaa neliöjuuren, saa euromääräisen arvion mallin mittavirheelle.
Päätät myös tutustua mallisi avulla löytämääsi ristiinvalidoinnin käsitteeseen ja vertailla malleja keskenään. Ristiinvalidointi varmistaa, että tuloksesi ei riipu jaostasi harjoitus- ja testidataan. Siinä jako suoritetaan useita kertoja ja jokaiselle kerralle lasketaan mallin mittavirhe. Näin varmistat, että saat luotettavan arvio mallisi mittavirheestä.
from sklearn.model_selection import cross_validate
# tehdään 10 jakoa ja lasketaan jokaiselle mittavirhe
# tulostetaan myös harjoitusjoukon mittavirhe. tämä on pienempi kuin testijoukon mittavirhe
cv_tulokset = cross_validate(linreg, X, y, cv = 10, scoring = 'neg_mean_squared_error',
return_train_score = True)
l_cv_tulokset = cross_validate(llinreg, logX, logy, cv = 10, scoring = 'neg_mean_squared_error',
return_train_score = True)
# katsotaan, mitä tuloksista saa irti
sorted(cv_tulokset.keys())
['fit_time', 'score_time', 'test_score', 'train_score']
# haetaan mallin antama harjoitusjoukkojen mittavirheet
cv_tulokset['test_score']
array([-153026.13614377, -110407.3034373 , -232558.70111822,
-146376.06503577, -429532.11077988, -85134.61473731,
-170797.56970554, -108400.32957821, -101579.73328116,
-593864.03571381])
l_cv_tulokset['test_score']
array([-0.22472328, -0.20672226, -0.17439947, -0.1132567 , -0.3115329 ,
-0.077125 , -0.57018558, -0.1788518 , -0.17820315, -0.91152702])
# lasketaan keskiarvo. vaihdetaan samalla merkkiä, jotta voidaan ottaa neliöjuuri
mse_linreg = - cv_tulokset['test_score'].mean()
mse_linreg
213167.65995309656
l_mse_linreg = - l_cv_tulokset['test_score'].mean()
l_mse_linreg
0.29465271497598833
rmse_linreg = np.sqrt(mse_linreg)
rmse_linreg
461.7008338232633
l_rmse_linreg = np.sqrt(l_mse_linreg)
l_rmse_linreg
0.5428192286350847
Mittavirheet eivät enää ole keskenään vertailukelpoisia. Huomataan, että tasomallin mittavirhe on melko suuri. Verrataan tätä vielä lopuksi yritysjohtajan keskipalkkaan, jotta saadaan selvä käsitys suuruusluokasta.
y.mean()
840.6761363636364
Toistetaan sama analyysi lassolle ja harjanneregressiolle. Vaihtelu virkistää, joten kokeilkaamme toista funktiota. Tämä tulostaa ainoastaan pyydetyt arvot testidatalle.
from sklearn.model_selection import cross_val_score
scores = cross_val_score(lasso, X, y, cv = 10, scoring = 'neg_mean_squared_error')
lscores = cross_val_score(llasso, logX, logy, cv = 10, scoring = 'neg_mean_squared_error')
rmse_lasso = np.sqrt(- scores.mean())
l_rmse_lasso = np.sqrt(- lscores.mean())
scores = cross_val_score(ridge, X, y, cv = 10, scoring = 'neg_mean_squared_error')
lscores = cross_val_score(lridge, logX, logy, cv = 10, scoring = 'neg_mean_squared_error')
rmse_ridge = np.sqrt(- scores.mean())
l_rmse_ridge = np.sqrt(- lscores.mean())
rmse_lasso
461.8945848042337
l_rmse_lasso
0.5676465567560017
rmse_ridge
461.66544606907047
l_rmse_ridge
0.5430121834217534
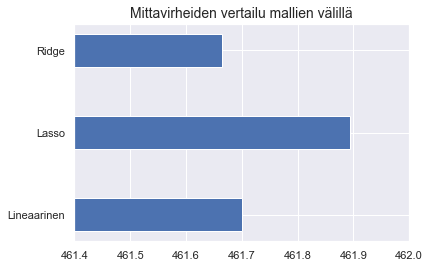
Säänneltyjen regressiomallien antama euromäärinen mittavirhe on samaa suuruusluokkaa tasomallille. Piirretän vielä asiaa havainnollistavat kuvat.
plt.barh(y = ['Lineaarinen', 'Lasso', 'Ridge'],
width = [rmse_linreg, rmse_lasso, rmse_ridge],
height = 0.4)
plt.xlim([461.4, 462])
plt.title("Mittavirheiden vertailu mallien välillä", fontsize = 14)
plt.show()
plt.barh(y = ['Lineaarinen', 'Lasso', 'Ridge'],
width = [l_rmse_linreg, l_rmse_lasso, l_rmse_ridge],
height = 0.4)
plt.xlim([0.54, 0.57])
plt.title("Mittavirheiden vertailu mallien välillä", fontsize = 14)
plt.show()
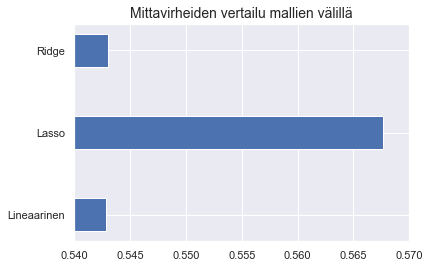
Lopulta päätät, että et missään tapauksessa voi käyttää malliasi arvioimaan potentiaalisten asiakkaittesi palkkaa nykytyössään. Huomaat kuitenkin, että analyysisi antaa tärkeää tietoa siitä, mitkä tekijät vaikuttavat yritysjohtajien palkkaan. Toivot, että tämä auttaisi sinua tulevaisuudessa löytämään paremmin kovapalkkaiset kandidaatit. Pohdit myös, pystyisikö mallisi rankkaamaan yritysjohtajat oikein palkan mukaan. Päätät palata vielä joskus asiaan paremmalla ajalla.
Lisämateriaalia: muuttujien skaalaaminen
Mallin selitysvoimaa voi parantaa skaalaamalla muuttujien arvoja yhtenäisempään mittakaavaan. Skaalaaminen on erityisen tärkeää silloin, kun muuttujien skaalat ovat kaukana toisistaan. Tässä mallissa skaalaaminen ei juurikaan vaikuta tuloksiin. Skaalaamisen vaikutuksiin voi tutustua allaolevan koodin avulla.
from sklearn.preprocessing import StandardScaler
scaler_x=StandardScaler()
scaler_y=StandardScaler()
X_scaled=scaler_x.fit_transform(X)
y_scaled=scaler_y.fit_transform(np.array(y).reshape(-1,1))
print(y_scaled.shape)
print(np.mean(X_scaled, axis=0))
print(np.mean(y_scaled, axis=0),np.std(y_scaled, axis=0))
(176, 1)
[ 3.93624527e-16 8.07434927e-17 1.00929366e-16 3.02788098e-17
-3.02788098e-17 -2.01858732e-17 1.00929366e-17 -7.31737903e-17
2.01858732e-17 0.00000000e+00]
[-2.01858732e-17] [1.]
/anaconda3/lib/python3.6/site-packages/sklearn/utils/validation.py:475: DataConversionWarning: Data with input dtype int64 was converted to float64 by StandardScaler.
warnings.warn(msg, DataConversionWarning)
/anaconda3/lib/python3.6/site-packages/sklearn/utils/validation.py:475: DataConversionWarning: Data with input dtype int64 was converted to float64 by StandardScaler.
warnings.warn(msg, DataConversionWarning)
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_scaled, random_state = 42)
linreg_scale = LinearRegression()
linreg_scale.fit(X_train, y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
linreg_scale.score(X_test, y_test)
0.16652837272427357
scaler_x=StandardScaler()
scaler_y=StandardScaler()
X_scaled=scaler_x.fit_transform(logX)
y_scaled=scaler_y.fit_transform(np.array(logy).reshape(-1,1))
print(y_scaled.shape)
print(np.mean(X_scaled, axis=0))
print(np.mean(y_scaled, axis=0),np.std(y_scaled, axis=0))
(176, 1)
[ 3.93624527e-16 8.07434927e-17 1.00929366e-16 3.02788098e-17
-2.01858732e-17 -2.57369883e-16 2.32137542e-16 -7.31737903e-17
2.01858732e-17 0.00000000e+00]
[1.56440517e-16] [1.]
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_scaled, random_state = 42)
linreg_scale = LinearRegression()
linreg_scale.fit(X_train, y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
linreg_scale.score(X_test, y_test)
0.10607108847310631
Lisätehtäviä
- Toista analyysi varioimalla käytettyjä muuttujia. Erityisesti toista tasomalli niin, että valitset vain toisen korreloituneista muuttujista.
- Toista analyysi siten, että mukana on johtaja, jolla on poikkeuksellisen korkea palkka. Logistisen mallin pitisi nyt selittää palkkaa jonkin verran paremmin, kun taas lineaarisen mallin selitysvoiman tulisi vähetä.