Tilastotieteen perusteita (Pythonilla)

Voit ladata materiaalin tästä Jupyter Notebookina.

import numpy as np
import pandas as pd
from IPython.display import display, Math, Latex
import matplotlib as mp
import scipy

Data sciencen yksi kivijaloista on tilastotiede ja sen menetelmät. Tarkoitus on tässä 1. workshopissa kerrata muutamia keskeisiä käsitteitä, ja syventää varsinaista menetelmäosaamista myöhemmissä sessioissa.

Sarjan 2. workshopissa käydään läpi tarkemmin Pythonia ja Pythonin datarakenteita, nyt vain siltä osin kuin on välttämätöntä laskuharjoituksien saamiseksi.

Olennaisena osana Pythonin käyttöä käytämme erilaisia kirjastoja (libraries). Näissä on paljon valmista koodia, jota voimme hyödyntää. Voisi ajatella, että käyttääksemme vaikkapa neliöjuurta, pitää tässäkin tietää, että mitä tapahtuu, mutta meidän ei tarvitse koko ajan kirjoittaa kaikkea koodia sen takana uudelleen, vaan voimme hyödyntää valmista käskyä, ja syöttää sille vain tarvittavaa dataa. Näihin kirjastoihin lukeutuvat mm. Scipy, Numpy, Pandas, Matplotlib ja lukuisia muita.

Kertausta keskeisiin tilastotieteen käsitteisiin

Mitä datatyyppejä on? Ja mitä niillä voi tehdä?

Riippuen datan luonteesta, voi sille tehdä operaatioita. Kaikkia operaatioita ei voi kuitenkaan suorittaa kuin tietyn tyyppiselle datalle/muuttujalle, riippuen muuttujan datan tyypistä.

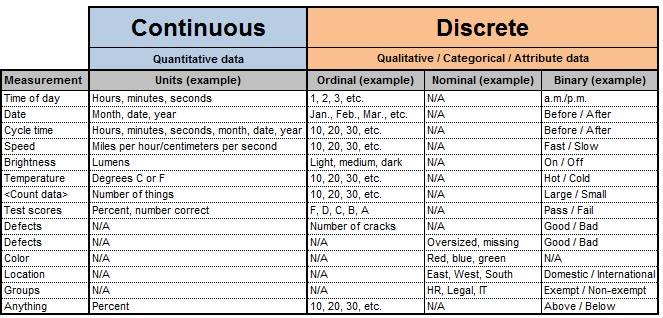
Diskreetit vs. jatkuvat muuttujat

Mikäli kyseessä on kvantitatiivinen muuttuja, niin nämä voidaan karkeasti jakaa kahteen tyyppiin:

1. Diskreetti muuttuja (muuttujan vaihtoehdot voidaan (helposti) luetella)
2. Jatkuva muuttuja (äärettömän(tai mahdottoman) paljon erilaisia arvoja tietyllä välillä

Usein tarkempana jakoperusteena käytetään e.m. esimerkkien lisäksi muuttujan tarkkuutta: jatkuvan muuttujan tarkkuutta voidaan parantaa, diskreetillä tarkkuuden parantaminen ei mahdollista/mielekästä.

Pohdintaa diskreetti vs. jatkuva

• Esim.lämpötila ilmiönä on jatkuva suure - mittaustulokset sen sijaan voivat näyttää diskreeteiltä johtuen resoluutiosta
• Aika, ikä, etäisyys,….

Toisaalta desimaalien olemassaolo (~suuri tarkkuus) datassa ei automaattisesti tarkoita, että muuttuja olisi jatkuva!

• Nopanheiton tulos 12,0000
• Peli, jossa kaksi voittomahdollisuutta ovat 5,5€ ja 10,11€

Erottelu jatkuva/diskreetti pääosin selvää, mutta joskus tulkinnanvaraista

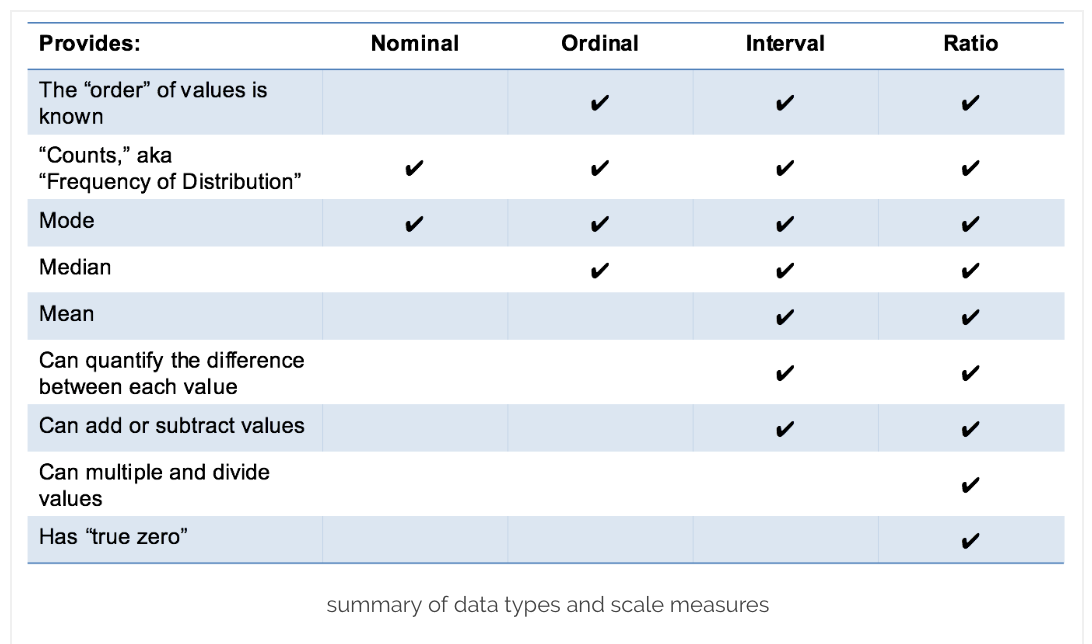
Mitta-asteikot

Erilaiset muuttujat kuuluvat ominaisuuksiensa perusteella erilaisiin mitta-asteikkoihin.

1. Nominaali‐/laatueroasteikko
2. Ordinaali‐/järjestysasteikko
3. Intervalli‐/välimatka‐asteikko
4. Relatiivi‐/suhdeasteikko.

Mitta‐asteikot pyrkivät kertomaan jotain muuttujan luonteesta tai suuruudesta verrattuna muihin havaintoihin. Mitta‐asteikkojen kohdalla on hyvä miettiä seuraavia asioita:

• Onko muuttujilla luonnollinen suuruusjärjestys?
• Mitä tarkoittaa x-yksikköä enemmän?
• Mitä tarkoittaa y‐kertainen?

Nominaaliasteikko

Nominaaliasteikosta käytetään myös nimeä luokittelu‐/laatueroasteikko. Muuttujilla ei ole selkeää suuruutta eikä suuruusjärjestystä.

Esimerkkejä?

Ordinaali- eli järjestysasteikko

Arvot voidaan järjestää mielekkäästi järjestykseen, mutta ”etäisyydet” peräkkäisten arvojen välillä eivät selkeästi mitattavissa, ts.havaintojen mittayksiköt ovat epäselvät.

Esimerkkejä?

Intervalli- eli välimatka-asteikko

Muuten vastaava kuin ordinaaliasteikko, mutta mittayksiköillä on selkeä tulkinta. Mittaa ilmiötä mielivaltaisesta nollapisteestä (=nollapiste on ns. sovittu). Soveltuu kvantitatiivisille muuttujille, joissa arvon xi suuruus perustuu välimatkaan (xi‐xj)toisesta pisteestä xj.

Esimerkkejä?

Suhde- eli relatiiviasteikko

Mittaa ilmiötä absoluuttisesta nollasta (voidaan nähdä myös erikoistapauksena intervalliasteikosta). Lukujen suhteet ovat informatiivisia. Nolla tarkoittaa, että ”ei ole yhtään” tarkasteltavaa suuretta

Esimerkkejä?

Keskiarvo, mediaani, moodi

Oppilaat saavat kokeista seuraavat arvosanat:

arvosanat = np.array([89,95,82,72,63,55,81,77,84,62,75,91,73,81,56,72,66,54,98,42,74,68,47,59,75,86])

Kuinka monta koetta opettajan piti arvostella?

len(arvosanat)

26

np.sort(arvosanat)

array([42, 47, 54, 55, 56, 59, 62, 63, 66, 68, 72, 72, 73, 74, 75, 75, 77,
       81, 81, 82, 84, 86, 89, 91, 95, 98])

print('Koeaineiston keskiarvo on') 
np.mean(arvosanat) 

Koeaineiston keskiarvo on





72.192307692307693

print ('Koeaineiston mediaani on ') 
np.median(arvosanat)

#Jos järjestetyn aineiston havaintojen lukumäärä on pariton, mediaani = keskimmäinen havainto. 
#Jos aineiston havaintojen lukumäärä on parillinen, on mediaani näiden kahden havainnon keskiarvo. 

Koeaineiston mediaani on 





73.5

Mitä mediaani tarkoittaa?

from scipy import stats

stats.mode(arvosanat)

ModeResult(mode=array([72]), count=array([2]))

Moodi on kyseisessä “arvosanat” aineistossa 72. Mitä se tarkoittaa?

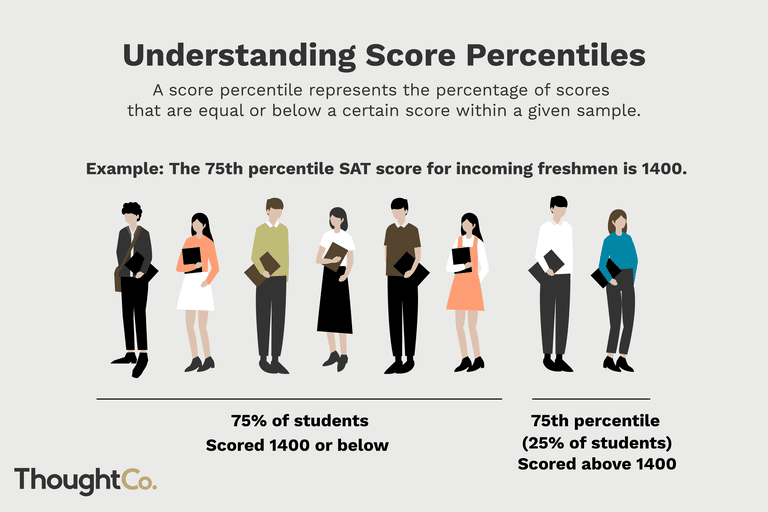
Percentiles (“prosenttipisteet”)

Mitä nämä ovat?

Prosenttipisteiden voisi ajatella olevan mediaanin sukulaisia.

Mediaani jakaa havaintojen lukumäärän perusteella 50%/50%, eli puolet havainnoista on mediaanin alapuolella, puolet yläpuolella.

Aineisto voidaan jakaa myös missä tahansa prosenttisuhteessa (lukumäärän perusteella). Prosenttilukemana annetaan pisteen ALAPUOLELLE jäävä prosenttiosuus.

Esim. 25% -piste tarkoittaa lukemaa, jonka alapuolelle jää 25% kaikista havainnoista.

• 25% -piste = alakvartiili (Q1)
• 75% -piste = yläkvartiili (Q3)

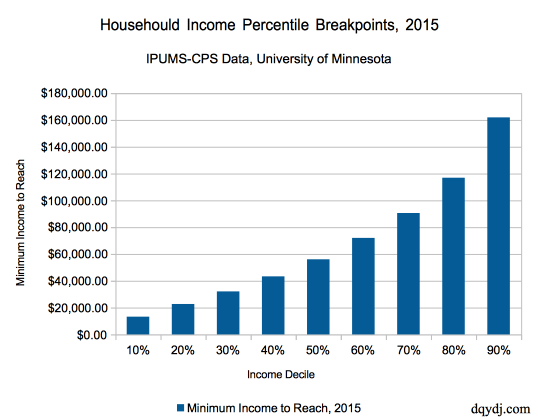
Desiilit ovat täysien 10-prosenttien mukaan määräytyvät kohdat:

• D1 = 10% -piste
• D2 = 20% -piste jne.

np.percentile(arvosanat, 50) #Tämä on sama kuin mediaani

73.5

np.percentile(arvosanat, 70) #30% opiskelijoista sai tätä KORKEAMMAN arvosanan

81.0

Varianssi ja keskihajonta

Varianssi ja keskihajonta ovat ns. hajontalukuja, jotka saavat sitä suuremmat arvot, mitä enemmän vaihtelua tarkasteltavassa aineistossa (muuttujassa) esiintyy. Yleensä tämä lasketaan mittaamalla havaittujen arvojen etäisyyttä havaintoarvojen odotus- tai keskiarvosta.

Varianssi

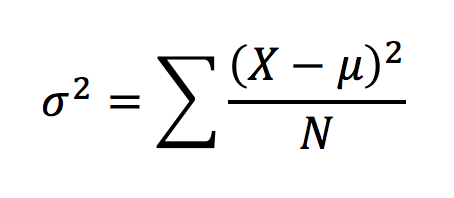
Arvon poikkeamaa keskiarvosta mitataan arvon ja keskiarvon erotuksen neliöllä (toinen potenssi). Erotuksen neliöistä lasketaan keskiarvo.

np.var(arvosanat)

203.84763313609469

Keskihajonnan avulla voi tarkastella paremmin absoluuttista hajontaa, sillä tulos on samalla asteikolla kuin muuttujan arvot. Keskihajonta on varianssin neliöjuuri.

np.std(arvosanat)

14.277521953619777

Normaalijakauma

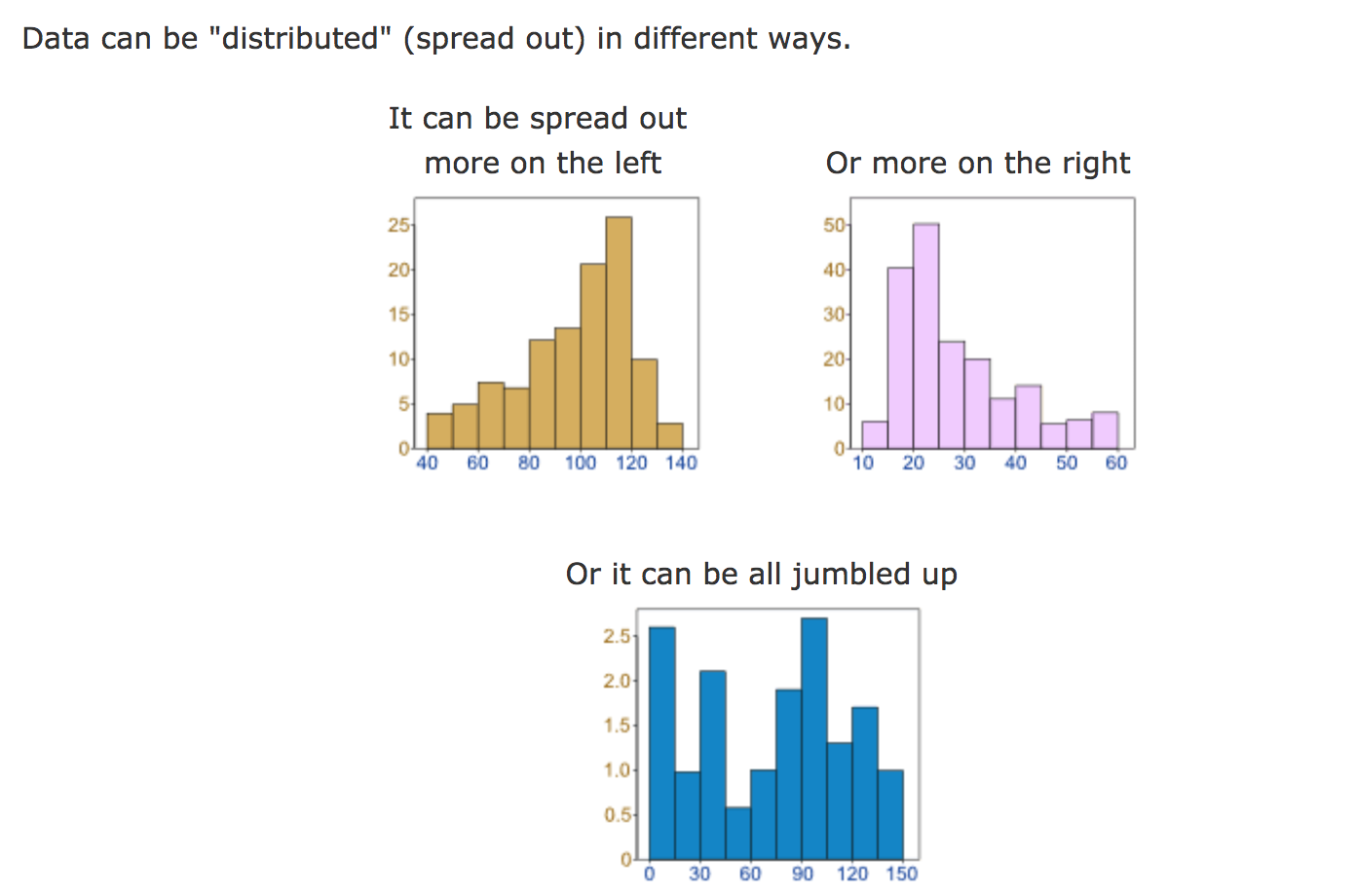
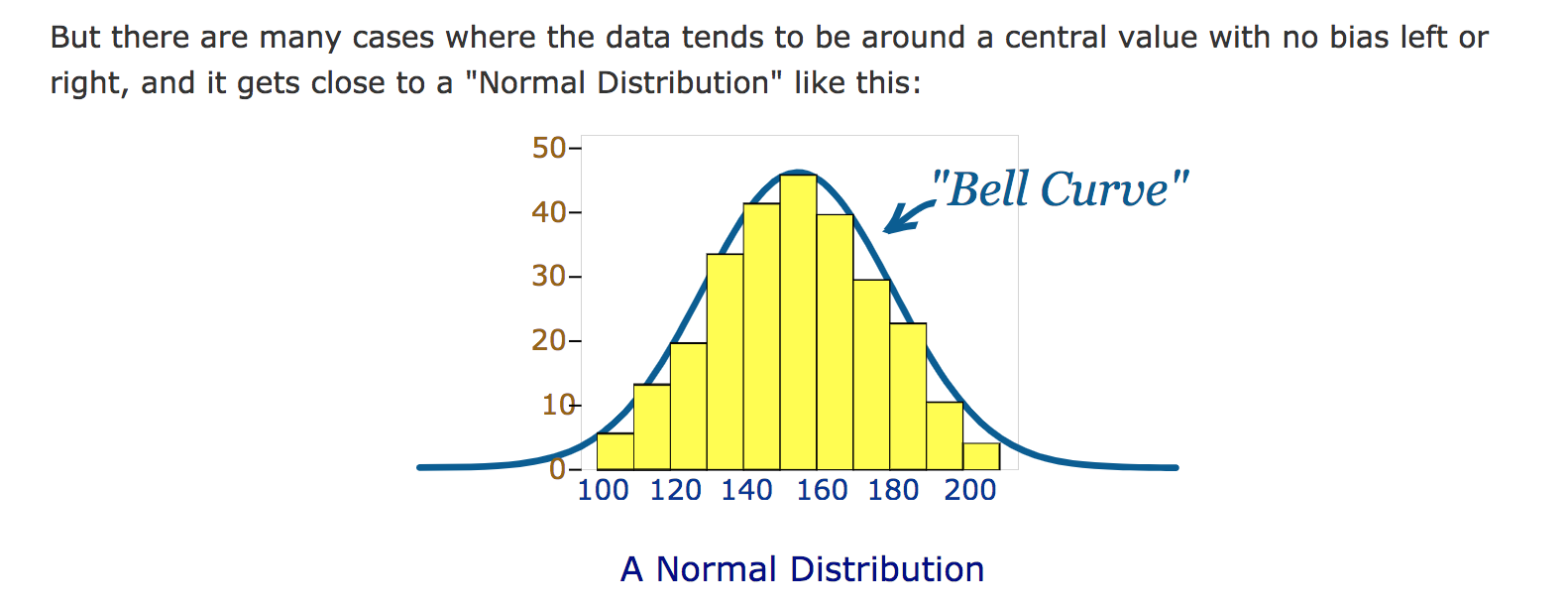
Mikäli muuttujan arvot ovat normaalijakautuneita, niin tällöin suurin osa havaintoja on lähellä keskiarvoja, ja mitä kauempana keskiarvosta tulos on, sitä epätodennäköisempää on muuttujan arvojen sijoittuminen e.m. “paikkaan”

Normaalijakaumaa noudattelevia muuttujia:

• Ihmisten pituudet
• Mittausvirheet
• Koetulokset
• Verenpaine
• Ihmisten älykkyysosamäärä ym.

Normaalijakaumaan liittyy kaksi olennaista arvoa, keskiarvo ja keskihajonta. Keskiarvo kuvaa jakauman huipun arvoa. Keskihajonnalla taas tarkoitetaan sitä, miten leveä käyrä on. Keskihajonnan pienentyessä käyrä myös kapenee. Noin kaksi kolmasosaa kaikista arvoista mahtuu keskihajonnan päähän keskiarvosta. Normitetussa normaalijakaumassa keskiarvo on 0 ja keskihajonta on 1. Tällaisessa tapauksessa siis kaksi kolmasosaa arvoista olisi -1 ja 1 välillä.